��Ŀ����
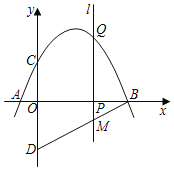
����Ŀ����ͼ��������y����![]() x2+
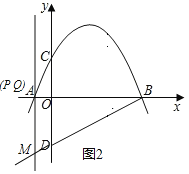
x2+![]() x+2��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���1���������ڵ�Q��
x+2��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���1���������ڵ�Q��
��1�����A����B����C�����ꣻ
��2������P���߶�OB���˶�ʱ��ֱ��1��ֱ��BD�ڵ�M����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ�
��3����P���߶�AB���˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A����1��0����B��4��0����C��0��2������2��m��2ʱ���ı���CQMD��ƽ���ı��Σ���3�����ڣ���Q��3��2����1��0����
��������
��1���������߹�ϵʽ�е�x��0��y��0���ֱ����y��x��ֵ�����������x�ᣬy��Ľ������ꣻ
��2����m��ʾ����Q��M�������꣬������ʾQM�ij���ʹCD��QM���������m��ֵ��
��3��������������н�𣬼��١�MBQ��90�����ڡ�MQB��90�����ۡ�QMB��90���ֱ���Ӧͼ�ν��н��
�⣺��1��������y����![]() x2+
x2+![]() x+2����x��0ʱ��y��2����˵�C��0,2����
x+2����x��0ʱ��y��2����˵�C��0,2����
��y��0ʱ��������![]() x2+
x2+![]() x+2��0�����x1��4��x2����1����˵�A����1,0����B��4,0����
x+2��0�����x1��4��x2����1����˵�A����1,0����B��4,0����
�ʣ�A����1,0����B��4,0����C��0,2����
��2���ߵ�D���C����x��Գƣ����D��0,��2����CD��4��
��ֱ��BD�Ĺ�ϵʽΪy��kx+b����D��0,��2����B��4,0������ã�
![]() ����ã�k��
����ã�k��![]() ��b����2��
��b����2��
��ֱ��BD�Ĺ�ϵʽΪy��![]() x��2
x��2
��M��m,![]() m��2����Q��m,��
m��2����Q��m,��![]() m2+
m2+![]() m+2����
m+2����
��QM����![]() m2+
m2+![]() m+2��
m+2��![]() m+2������
m+2������![]() m2+m+4��
m2+m+4��
��QM��CDʱ���ı���CQMD��ƽ���ı��Σ�
�ੁ![]() m2+m+4��4��
m2+m+4��4��
���m1��0����ȥ����m2��2��
��m��2ʱ���ı���CQMD��ƽ���ı��Σ�
��3����Rt��BOD��OD��2��OB��4�����OB��2OD��
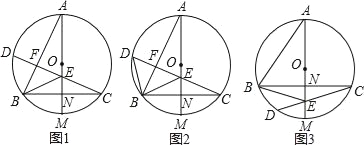
������MBQ��90��ʱ����ͼ1��ʾ��
����QBM�ס�BODʱ��QP��2PB��
���P�ĺ�����Ϊx����QP����![]() x2+
x2+![]() x+2��PB��4��x��
x+2��PB��4��x��
���ǩ�![]() x2+
x2+![]() x+2��2��4��x����
x+2��2��4��x����
��ã�x1��3��x2��4����ȥ����
��x��3ʱ��PB��4��3��1��
��PQ��2PB��2��
���Q��������3��2����
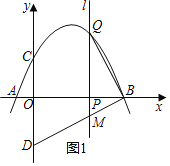
������MQB��90��ʱ����ͼ2��ʾ����ʱ��P��Q���A�غϣ�
��Q����1��0����
�����ڵ�M��ֱ��BD�ϣ���ˡ�QMB��90����������������ڡ�QBM�ס�BOD��
������������P���߶�AB���˶������У����ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ�
��Q��3��2����1��0����