题目内容
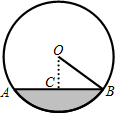 一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是
一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是
- A.16
- B.10
- C.8
- D.6
A
分析:先根据垂径定理得出AB=2BC,再根据勾股定理求出BC的长,进而可得出答案.
解答:∵截面圆圆心O到水面的距离OC是6,
∴OC⊥AB,
∴AB=2BC,
在Rt△BOC中,OB=10,OC=6,
∴BC= =
=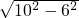 =8,
=8,
∴AB=2BC=2×8=16.
故选A.
点评:本题考查的是垂径定理的应用,熟知垂径定理及勾股定理是解答此题的关键.
分析:先根据垂径定理得出AB=2BC,再根据勾股定理求出BC的长,进而可得出答案.
解答:∵截面圆圆心O到水面的距离OC是6,
∴OC⊥AB,
∴AB=2BC,
在Rt△BOC中,OB=10,OC=6,
∴BC=
 =
=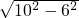 =8,
=8,∴AB=2BC=2×8=16.
故选A.
点评:本题考查的是垂径定理的应用,熟知垂径定理及勾股定理是解答此题的关键.

练习册系列答案
相关题目
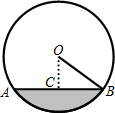 一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )
一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )| A、16 | B、10 | C、8 | D、6 |
 一条排水管的截面如图所示,已知排水管的截面半径OB=5,截面圆圆心为O,当水面宽AB=8时,水位高是多少( )
一条排水管的截面如图所示,已知排水管的截面半径OB=5,截面圆圆心为O,当水面宽AB=8时,水位高是多少( )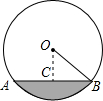 (2013•丽水)一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
(2013•丽水)一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )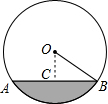 (2012•湛江模拟)一条排水管的截面如图所示,已知排水管的截面圆半径OB=5,截面圆圆心O到水面的距离OC是3,则水面宽AB是( )
(2012•湛江模拟)一条排水管的截面如图所示,已知排水管的截面圆半径OB=5,截面圆圆心O到水面的距离OC是3,则水面宽AB是( )