题目内容
 (1)解方程:
(1)解方程:| 1 |
| x+1 |
| 2 |
| x-1 |
| 7 |
| x2-1 |
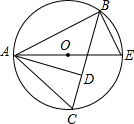
(2)如图所示,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE.求 证:△ABE∽△ADC.
分析:(1)先去分母,然后通过移项、合并同类项,化未知数的系数为1;注意需要验根.
(2)由AE是直径可得∠ABE是直角,所以∠ABE=∠ADC,由∠C、∠E是同弧AB^所对的圆周角可得∠C=∠E,所以△ABE与△ADC相似.
(2)由AE是直径可得∠ABE是直角,所以∠ABE=∠ADC,由∠C、∠E是同弧AB^所对的圆周角可得∠C=∠E,所以△ABE与△ADC相似.
解答:解:(1)由原方程,得
x-1+2x+2=7,即3x=6,
解得,x=2;
将x=2代入原方程,经检验x=2是原方程的根;

(2)在△ABE与△ADC中,
∵AE是⊙O的直径,∴∠ABE=90°,
∵AD是△ABC的边BC上的高,
∴∠ADC=90°,∴∠ABE=∠ADC;
又∵同弧所对的圆周角相等,∴∠BEA=∠DCA,
∴△ABE∽△ADC.
x-1+2x+2=7,即3x=6,
解得,x=2;
将x=2代入原方程,经检验x=2是原方程的根;

(2)在△ABE与△ADC中,
∵AE是⊙O的直径,∴∠ABE=90°,
∵AD是△ABC的边BC上的高,
∴∠ADC=90°,∴∠ABE=∠ADC;
又∵同弧所对的圆周角相等,∴∠BEA=∠DCA,
∴△ABE∽△ADC.
点评:本题综合考查了圆周角定理、相似三角形的判定以及解分式方程.解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解;解分式方程一定注意要验根.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目