��Ŀ����
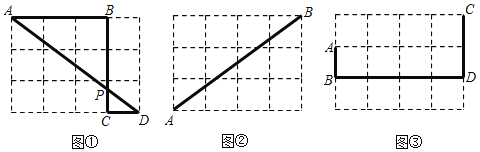
����Ŀ����ͼ����Rt��ABC�У���A��90����AC��3��AB��4������P�ӵ�A��������AB������ÿ��2����λ���ȵ��ٶ����յ�B�˶�����QΪ�߶�AP���е㣬����P������PM��AB����PM��3AQ����PQ��PMΪ��������PQNM�����P���˶�ʱ��Ϊt�룮
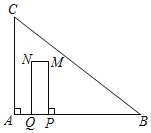
��1���߶�MP�ij�Ϊ�� �����ú�t�Ĵ���ʽ��ʾ����
��2�����߶�MN���BC�й�����ʱ����t��ȡֵ��Χ��
��3������N����ABC�ڲ�ʱ�������PQNM����ABC�ص�����ͼ�ε����ΪS����S��t֮��ĺ�����ϵʽ��
��4������M����ABC������������ֱ�߾������ʱ��ֱ��д����ʱt��ֵ��
���𰸡���1��3t����2������������t��ֵΪ![]() ��t��
��t��![]() ����3��S��
����3��S��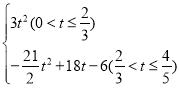 ����4������������t��ֵΪ
����4������������t��ֵΪ![]() ��
��![]() ��
��![]() .
.
��������
��1������·�̡��ٶȡ�ʱ��Ĺ�ϵ�ٽ��������.
��2���ֱ����M��N����BC��ʱ��t�ķ�Χ���ɣ�
��3�����ص������Ǿ���PQNM�������PQNEF����������н�ɣ�
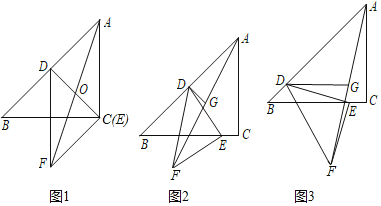
��4���������������Σ�����M���ڡ�ABC�Ľ�ƽ����BF��ʱ����������.��FELBC��E������M���ڡ�ACB�Ľ�ƽ������ʱ������������EFLBC��F������M���ڡ�ABC�ġ�ACB����ǵ�ƽ������ʱ����������.�ֱ���⼴�ɽ��.
�⣺��1��������AP��2t��AQ��PQ��t��
��PM��3PQ��
��PM��3t��
�ʴ�Ϊ3t��
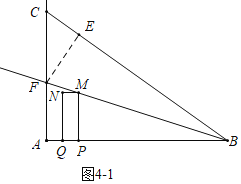
��2����ͼ2��1�У�����M����BC��ʱ��
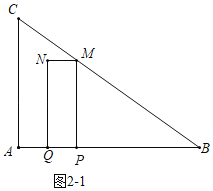
��PM��AC��
��![]() ��
��
��![]() ��
��
���t��![]()
��ͼ2��2�У�����N����BC��ʱ��
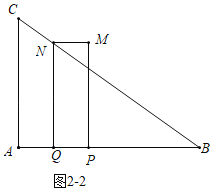
��NQ��AC��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
��������������������t��ֵΪ![]() ��t��
��t��![]() ��
��
��3����ͼ3��1�У���0��t��![]() ʱ���ص������Ǿ���PQNM��S��3t2
ʱ���ص������Ǿ���PQNM��S��3t2
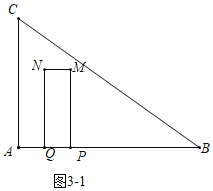
��ͼ3��2�У���![]() ��t��
��t��![]() ʱ���ص������������PQNEF��
ʱ���ص������������PQNEF��
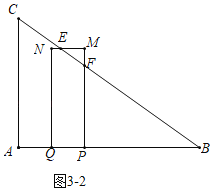
S��S����PQNM��S��EFM��3t2��![]() [3t��
[3t��![]() ��4��2t��]
��4��2t��]![]() [3t��
[3t��![]() ��4��2t��]����
��4��2t��]����![]() t2+18t��6��
t2+18t��6��
����������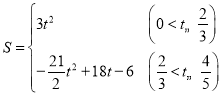 ��
��
��4����ͼ4��1�У�����M���ڡ�ABC�Ľ�ƽ����BF��ʱ��������������FE��BC��E��
�ߡ�FAB����FEB��90�㣬��FBA����FBE��BF��BF��
���BFA�ա�BFE��AAS����
��AF��EF��AB��BE��4����AF��EF��x��
�ߡ�A��90�㣬AC��3��AB��4��
��BC��![]() ��5��
��5��
��EC��BC��BE��5��4��1��
��Rt��EFC������x2+12����3��x��2��
���x��![]() ��
��
��PM��AF��
��![]() ��
��
��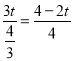 ��
��
��t��![]()
��ͼ4��2�У�����M���ڡ�ACB�Ľ�ƽ������ʱ������������EF��BC��F��
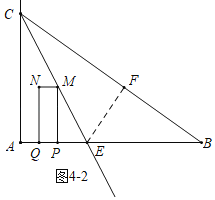
ͬ����֤����ECA�ա�ECF��AAS����
��AE��EF��AC��CF��3����AE��EF��y��
��BF��5��3��2��
��Rt��EFB������x2+22����4��x
���x��![]() ��
��
��PM��AC��
��![]() ��
��
��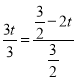 ��
��
���t��![]() ��
��
��ͼ4��3�У�����M���ڡ�ABC�ġ�ACB����ǵ�ƽ������ʱ������������
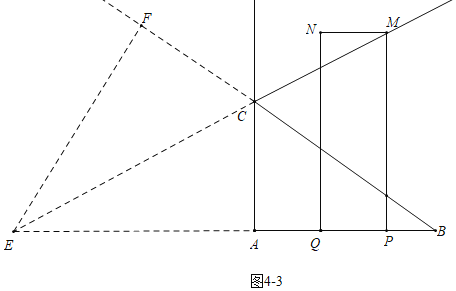
��MC���ӳ��߽�BA���ӳ�����E����EF��BC��BC���ӳ����ڷ֣�
ͬ����֤��AC��CF��3��EF��AE����EF��EA��x��
��Rt��EFB������x2+82����x+4��2��
���x��6��
��AC��PM��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
��������������������t��ֵΪ![]() ��
��![]() ��
��![]() .
.

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�