题目内容
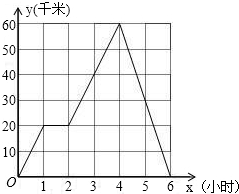
 小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(小时)的函数图象如图.
小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(小时)的函数图象如图.(1)小张在路上停留
1
1
小时,他从乙地返回时骑车的速度为30
30
千米/时.(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程y(千米)与时间x(小时)的函数的大致图象.
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程y(千米)与时间x(小时)的函数关系式为y=12x+10.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
分析:(1)根据图象直接得出小张在路上停留以及返回时速度即可;
(2)利用途中小李与小张共相遇3次画出图象即可;
(3)将两函数联立求出交点横坐标即可得出答案.
(2)利用途中小李与小张共相遇3次画出图象即可;
(3)将两函数联立求出交点横坐标即可得出答案.
解答: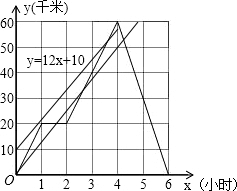 解:(1)如图所示:小张在路上停留1小时,
解:(1)如图所示:小张在路上停留1小时,
他从乙地返回时骑车的速度为60÷=30(千米/时).
故答案为:1,30;
(2)如图所示:
要求图象能正确反映起点与终点;
(3)由函数y=12x+10的图象可知,小王与小张在途中共相遇2次,
并在出发后2小时到4小时之间第一次相遇.
当2≤x≤4时,y=20x-20.
由
,
得x=
,
所以第一次相遇的时间为
小时.
 解:(1)如图所示:小张在路上停留1小时,
解:(1)如图所示:小张在路上停留1小时,他从乙地返回时骑车的速度为60÷=30(千米/时).
故答案为:1,30;
(2)如图所示:
要求图象能正确反映起点与终点;
(3)由函数y=12x+10的图象可知,小王与小张在途中共相遇2次,
并在出发后2小时到4小时之间第一次相遇.
当2≤x≤4时,y=20x-20.
由
|
得x=
| 15 |
| 4 |
所以第一次相遇的时间为
| 15 |
| 4 |
点评:此题主要考查了一次函数的应用以及二元一次方程组的应用,利用图象分析得出是解题关键.

练习册系列答案
相关题目
 (1)小张在路上停留
(1)小张在路上停留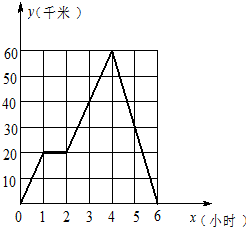 小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.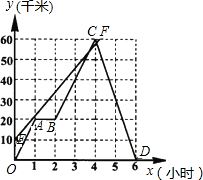 算过程.
算过程. (千米)与时间
(千米)与时间 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.
 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.