题目内容
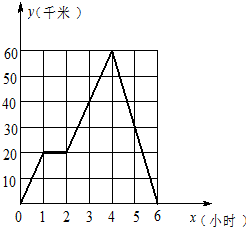 小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.(1)小张在路上停留
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=12x+10.小王与小张在途中共相遇
分析:(1)观察图不难发现,小张在路上停留1小时;根据汽车的速度=
求得结果.
(2)从图中发现不难发现小张与小王共相遇2次.
设小张在2≤x≤4函数关系式为y=kx+b,从图中不难找到小张行进在该段上的两点(2,20)、(4,60),将这两点坐标值代入上式,求得k、b的值,从而确定小张在2≤x≤4时的函数关系式.再联立小王的行进函数关系式,解得x的值,即为所求值.
| 甲乙两地的路程 |
| 从乙地返回甲地用时 |
(2)从图中发现不难发现小张与小王共相遇2次.
设小张在2≤x≤4函数关系式为y=kx+b,从图中不难找到小张行进在该段上的两点(2,20)、(4,60),将这两点坐标值代入上式,求得k、b的值,从而确定小张在2≤x≤4时的函数关系式.再联立小王的行进函数关系式,解得x的值,即为所求值.
解答:解:(1)由图中可知,
小张在路上停留1小时,他从乙地返回时骑车的速度=
=30(千米/时);
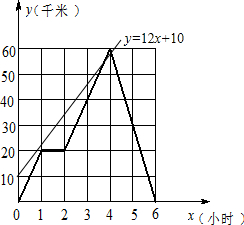 (2)小王与小张在途中共相遇2次.
(2)小王与小张在途中共相遇2次.
设小张在2≤x≤4函数关系式为y=kx+b,
,解得k=20、b=-20,
∴小张在2≤x≤4函数关系式y=20x-20,
,
解得:x=
.
答:(1)1,30;
(2)2,出发后
小时第一次相遇.
小张在路上停留1小时,他从乙地返回时骑车的速度=
| 60 |
| 6-4 |
 (2)小王与小张在途中共相遇2次.
(2)小王与小张在途中共相遇2次.设小张在2≤x≤4函数关系式为y=kx+b,
|
∴小张在2≤x≤4函数关系式y=20x-20,
|
解得:x=
| 15 |
| 4 |
答:(1)1,30;
(2)2,出发后
| 15 |
| 4 |
点评:本题考查一次函数的应用.解决本题的关键是同学们一定要弄明白他们在行进过程中的具体关系,画出函数关系图;再就是要学会运用图象中的特殊点,比如本题中的点(2,20)、(4,60).

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
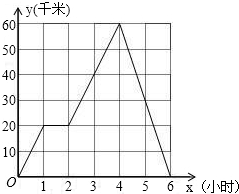 (1)小张在路上停留
(1)小张在路上停留 小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(小时)的函数图象如图.
小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(小时)的函数图象如图.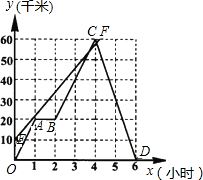 算过程.
算过程. (千米)与时间
(千米)与时间 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.
 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.