题目内容
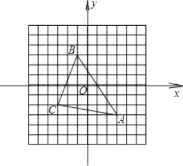
【题目】已知抛物线y=ax2+2x+c的图象与x轴交于点A（3，0）和点C，与y轴交于点B（0，3）．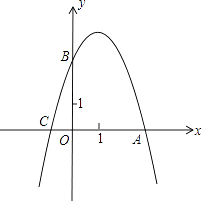
（1）求抛物线的解析式；
（2）在抛物线的对称轴上找一点D，使得点D到点B、C的距离之和最小，并求出点D的坐标解：；
（3）在第一象限的抛物线上，是否存在一点P，使得△ABP的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵抛物线y=ax2+2x+c的图象经过点A（3，0）和点B（0，3），
∴ 
，解得a=﹣1，c=3，
∴抛物线的解析式为：y=﹣x2+2x+3．
（2）
对称轴为x= 
=1，
令y=﹣x2+2x+3=0，解得x1=3，x2=﹣1，∴C（﹣1，0）．
如图1所示，连接AB，与对称轴x=1的交点即为所求之D点，由于A、C两点关于对称轴对称，则此时DB+DC=DB+DA=AB最小．
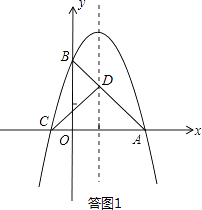
设直线AB的解析式为y=kx+b，由A（3，0）、B（0，3）可得：
，解得k=﹣1，b=3，
∴直线AB解析式为y=﹣x+3．
当x=1时，y=2，∴D点坐标为（1，2）．
（3）
解：结论：存在．
如图2所示，
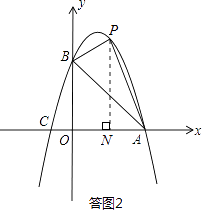
设P（x，y）是第一象限的抛物线上一点，
过点P作PN⊥x轴于点N，则ON=x，PN=y，AN=OA﹣ON=3﹣x．
S△ABP=S梯形PNOB+S△PNA﹣S△AOB
= 
（OB+PN）ON+ PNAN﹣ OAOB
= （3+y）x+ y（3﹣x）﹣ ×3×3
= 
（x+y）﹣ 
，
∵P（x，y）在抛物线上，∴y=﹣x2+2x+3，代入上式得：
S△ABP= （x+y）﹣ =﹣ （x2﹣3x）=﹣ （x﹣ ）2+ 
，
∴当x= 时，S△ABP取得最大值．
当x= 时，y=﹣x2+2x+3= 
，∴P（ 
， ）．
所以，在第一象限的抛物线上，存在一点P，使得△ABP的面积最大；P点的坐标为（ ， ）．
【解析】（1）利用待定系数法求出抛物线的解析式；（2）连接AB，与对称轴x=1的交点即为所求之D点．为求D点坐标，需先求出直线AB的解析式，然后令x=1求得y，即可求出D点坐标；（3）本问关键是求出△ABP的面积表达式．这个表达式是一个关于P点横坐标的二次函数，利用二次函数求极值的方法可以确定P点的坐标．
【考点精析】掌握二次函数的性质是解答本题的根本，需要知道增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
