题目内容
【题目】如图，在Rt△ABC中，∠ACB=90° ，AC=3，BC=6，点D在AB上，AD=AC， AF⊥CD交CD于点E，交CB于点F，则CF的长是____.
【答案】
【解析】
在Rt△ABC中，用勾股定理可求AB=
，连接DF，易得AF为CD的中垂线，可得DF=CF，再证明△ADF≌△ACF，得∠ADF=90°，设CF=x，在Rt△BDF中用勾股定理建立方程即可求解.
解：如图所示，连接DF，
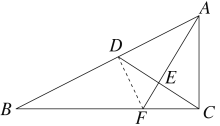
在Rt△ABC中，
，
∵AD=AC，AF⊥CD，
∴AF垂直平分CD，∴DF=CF
在△ADF和△ACF中
∴△ADF≌△ACF（SSS）
∴∠ADF=∠ACF=90°
设CF=x，则DF=x，BF=6-x，
在Rt△BDF中，
由勾股定理得BD+DF=BF
即
解得
练习册系列答案
相关题目
