题目内容
如图,以正方形ABCD的边CD为直径作⊙O,以顶点C为圆心、边CB为半径作 |
| BD |
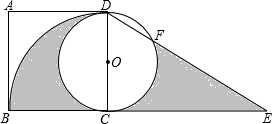 的延长线上一点,且CD、CE的长恰为方程x2-2(
的延长线上一点,且CD、CE的长恰为方程x2-2(| 3 |
| 3 |
(1)求DF的长;
(2)求图中阴影部分的面积S.
分析:(1)先根据CD、CE的长恰为方程x2-2(
+1)x+4
=0的两根,求出CD、CE的长;再根据CD、CE的长求出∠CDE的正切值,进而求出∠CDE的度数;然后利用直角三角形的特点求出DF的长.
(2)由图形可知S阴影=(S扇形BCD-
S⊙O)+(S△DCE-S△DOF-S扇形COF),然后根据面积计算公式计算即可.
| 3 |
| 3 |
(2)由图形可知S阴影=(S扇形BCD-
| 1 |
| 2 |
解答:解:(1)连接CF,
∵CD、CE的长为方程x2-2(
+1)x+4
=0的两根;
∴CE=2
,CD=2;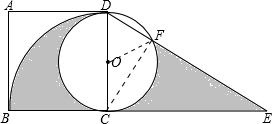
∵∠DCE=90°,
∴tan∠CDE=
=
;
∴∠CDE=60°;
∵CD是⊙O的直径,
∴∠DFC=90°;
∴DF=
DC=
×2=1.
(2)连接OF,
∵∠CDE=60°,OD=OF,
∴△DOF是等边三角形;
∴OD=OF=DF=1;
∴S△DOF=
×1=
,S扇形FOC=
=
,
S阴影FEC=S△ECD-S△DOF-S扇形FOC=
×2×2
-
-
=
-
,
S阴影DBC=S扇形BCD-S半圆O=
-
π×1=
π,
∴S阴影=S阴影FCE+S阴影DBC=
-
+
π,
=
+
.
∵CD、CE的长为方程x2-2(
| 3 |
| 3 |
∴CE=2
| 3 |

∵∠DCE=90°,
∴tan∠CDE=
| CE |
| CD |
| 3 |
∴∠CDE=60°;
∵CD是⊙O的直径,
∴∠DFC=90°;
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接OF,
∵∠CDE=60°,OD=OF,
∴△DOF是等边三角形;
∴OD=OF=DF=1;
∴S△DOF=
| ||
| 4 |
| ||
| 4 |
| 120π×12 |
| 360 |
| π |
| 3 |
S阴影FEC=S△ECD-S△DOF-S扇形FOC=
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| π |
| 3 |
7
| ||
| 4 |
| π |
| 3 |
S阴影DBC=S扇形BCD-S半圆O=
| 90π×22 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S阴影=S阴影FCE+S阴影DBC=
7
| ||
| 4 |
| π |
| 3 |
| 1 |
| 2 |
=
7
| ||
| 4 |
| π |
| 6 |
点评:本题考查了正方形的性质、扇形面积的计算方法等知识.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.

练习册系列答案
相关题目
 13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=
13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=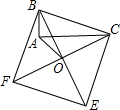 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO= 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( ) 如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )
如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )