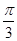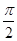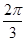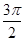题目内容
在⊙O中AB为弦,∠AOB=90°,点O到AB的距离为5,则⊙O的半径为______.
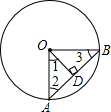
如图,在⊙O中AB为弦,∠AOB=90°,OD⊥AB,且OD=5.
∵OA=OB,OD⊥AB,∠AOB=90°,
∴∠1=
∠AOB=45°,∠2=∠3=45°,
∴∠1=∠2,
∴OD=AD=5,
∴直角△ADO中,由勾股定理得到:OA=
=5
.
故答案是:5
.
∵OA=OB,OD⊥AB,∠AOB=90°,
∴∠1=
| 1 |
| 2 |
∴∠1=∠2,
∴OD=AD=5,
∴直角△ADO中,由勾股定理得到:OA=
| OD2+AD2 |
| 2 |
故答案是:5
| 2 |


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

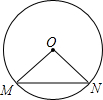



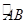 的长等于( )
的长等于( )