题目内容
【题目】已知： 
， 
与
成正比例， 
与
成反比例，并且
时， 
； 
时， 
．求
时， 
的值．
解：由
与
成正比例， 
与
成反比例，可设
， 
，又
，
所以
．把
， 
代入上式，解得
． 
．
当
时， 
．
阅读上述解答过程，其过程是否正确，若不正确，请说明理由，并给出正确的解题过程．
【答案】见解析
【解析】试题分析：两个函数比例系数不同，在设的过程中应该体现出来.由于y1与x成正比例，y2与x成反比例，则可以设y1=k1x，y2=
（k1≠0，k2≠0），结合题意y=y1+y2，可得y=k1x+
；根据题意可把x=1，y=4；x=3，y=5分别代入y=k1x+
中，得到一个二元一次方程组，解出k1、k2的值，至此可得y与x的函数关系式；
根据所得的解析式，再将x=4代入其中，至此可求出y的值.
试题解析：其解答过程是错误的。
∵正比例函数y1=k1x，与反比例函数y2=
x的k值不一定相等，故设y1=k1x，y2=
（k1≠0，k2≠0）.
∵y=y1+y2，
∴y=k1x+
.
把
， 
的值代入得
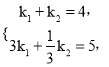解得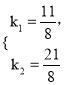
．
∴当x=4时，y=
．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
