题目内容
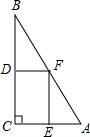 (2013•仓山区模拟)(1)如图,在△ABC中,∠C=90°,BC>AC,点D、E、F分别是△ABC三边的中点,求证:四边形DCEF是矩形.
(2013•仓山区模拟)(1)如图,在△ABC中,∠C=90°,BC>AC,点D、E、F分别是△ABC三边的中点,求证:四边形DCEF是矩形.(2)有一个两位数,它的十位上的数字与个位上的数字之和为10,差为6,求这个两位数.
分析:(1)根据三角形中位线的性质得出DF∥AC,EF∥DC,进而利用平行线的性质得出,∠CEF=90°,∠CDF=90°,即可得出四边形DCEF是矩形;
(2)根据题意设个位上的数字x,则十位上的数字是x+6,再根据“个位与十位上的数字之和是10”列方程求解.
(2)根据题意设个位上的数字x,则十位上的数字是x+6,再根据“个位与十位上的数字之和是10”列方程求解.
解答:(1)证明:∵点D、E、F分别是△ABC三边的中点,
∴DF∥AC,EF∥DC,
∵∠C=90°,
∴∠CEF=90°,∠CDF=90°,
∴四边形DCEF是矩形.
(2)解:设个位上的数字x,则十位数字是x+6,由题意可得:
x+x+6=10,
2x=4,
解得:x=2;
十位数字是:x+6=2+6=8,
则这个两位数是82.
∴DF∥AC,EF∥DC,
∵∠C=90°,
∴∠CEF=90°,∠CDF=90°,
∴四边形DCEF是矩形.
(2)解:设个位上的数字x,则十位数字是x+6,由题意可得:
x+x+6=10,
2x=4,
解得:x=2;
十位数字是:x+6=2+6=8,
则这个两位数是82.
点评:此题主要考查了矩形的判定和一元一次方程的应用,利用等量关系表示出个位数和十位数之间的关系是解题关键.

练习册系列答案
相关题目
 (2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( )
(2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( ) (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是 (2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.
(2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.