题目内容
 (2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.
(2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.(1)求抛物线解析式;
(2)连接AC,过点A做AC的垂线交抛物线于点D,交对称轴于E,求直线AD的解析式;
(3)在(2)的条件下,连接BD,若点P在x轴正半轴,且以A、E、P为顶点的三角形与△ABD相似,求出所有满足条件的P点坐标.
分析:(1)可设该抛物线解析式为顶点式y=a(x-2)2-1.把点A的坐标代入来求a的值即可;
(2)根据点A、C的坐标求得∠FAC=45°,则∠DAB=45°,故可设直线AD的解析式为y=x+b.把点A的坐标代入并求得b的值;
(3)以A、E、P为顶点的三角形与△ABD相似,对于这两个三角形的对应角与对应边没有明确的情况下,需要分类讨论:①如图1,当△ABD∽△AEP时;②如图2,当△ABD∽△APE时;③如图3,当△ABD∽△PAE时.根据这些相似三角形的对应边成比例可以求得线段AP的长度.
(2)根据点A、C的坐标求得∠FAC=45°,则∠DAB=45°,故可设直线AD的解析式为y=x+b.把点A的坐标代入并求得b的值;
(3)以A、E、P为顶点的三角形与△ABD相似,对于这两个三角形的对应角与对应边没有明确的情况下,需要分类讨论:①如图1,当△ABD∽△AEP时;②如图2,当△ABD∽△APE时;③如图3,当△ABD∽△PAE时.根据这些相似三角形的对应边成比例可以求得线段AP的长度.
解答: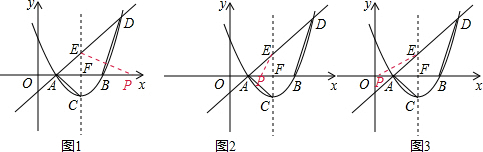 解:(1)∵已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),
解:(1)∵已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),
∴设该抛物线解析式为y=a(x-2)2-1(a≠0).
把点A(1,0)代入,
解得a=1,
∴该函数解析式为:y=(x-2)2-1.(或y=x2-4x+3).
(2)∵由(1)知,该函数解析式为:y=(x-2)2-1=(x-1)(x-3),
即y=(x-1)(x-3),
∴A(1,0).
∵顶点坐标是C(2,-1),CF是对称轴,
∴AF=CF=1,∠AFC=90°,
∴∠FAC=45°,
∵AC⊥AD,
∴∠DAB=45°,故可设直线AD的解析式为y=x+b.
把点A(1,0)代入,
解得b=-1,
∴直线AD的解析式为y=x-1.
(3)∵由(2)知,∠DAB=45°,即∠EAF=45°,
∴在直角△AEF中,∠EAF=∠AEF=45°,
∴AF=EF=1,
∴AE=
,AB=2.
∵点D的抛物线y=x2-4x+3与直线ADy=x-1的交点,
∴
,
解得,
(不合题意,舍去),或
,
∴D(4,3),
∴AD=3
,BD=
①如图1,当△ABD∽△AEP时,
=
,即
=
,
解得AP=3,
∴P(4,0);
②如图2,当△ABD∽△APE时,
=
,即
=
,解得:AP=
,∴P(
,0);
③如图3,当△ABD∽△PAE时,
=
,即
=
,解得,AP=
,∴P(1-
,0).
综上所述,满足条件的点P的坐标是(4,0)、(
,0)和(1-
,0).
 解:(1)∵已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),
解:(1)∵已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),∴设该抛物线解析式为y=a(x-2)2-1(a≠0).
把点A(1,0)代入,
解得a=1,
∴该函数解析式为:y=(x-2)2-1.(或y=x2-4x+3).
(2)∵由(1)知,该函数解析式为:y=(x-2)2-1=(x-1)(x-3),
即y=(x-1)(x-3),
∴A(1,0).
∵顶点坐标是C(2,-1),CF是对称轴,
∴AF=CF=1,∠AFC=90°,
∴∠FAC=45°,
∵AC⊥AD,
∴∠DAB=45°,故可设直线AD的解析式为y=x+b.
把点A(1,0)代入,
解得b=-1,
∴直线AD的解析式为y=x-1.
(3)∵由(2)知,∠DAB=45°,即∠EAF=45°,
∴在直角△AEF中,∠EAF=∠AEF=45°,
∴AF=EF=1,
∴AE=
| 2 |
∵点D的抛物线y=x2-4x+3与直线ADy=x-1的交点,
∴
|
解得,
|
|
∴D(4,3),
∴AD=3
| 2 |
| 10 |
①如图1,当△ABD∽△AEP时,
| AB |
| AE |
| AD |
| AP |
| 2 | ||
|
3
| ||
| AP |
解得AP=3,
∴P(4,0);
②如图2,当△ABD∽△APE时,
| AE |
| AD |
| AP |
| AB |
| ||
3
|
| AP |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
③如图3,当△ABD∽△PAE时,
| AB |
| PA |
| BD |
| AE |
| 2 |
| PA |
| ||
|
2
| ||
| 5 |
2
| ||
| 5 |
综上所述,满足条件的点P的坐标是(4,0)、(
| 4 |
| 3 |
2
| ||
| 5 |
点评:本题考查了二次函数综合题.其中涉及到的知识点有待定系数法求一次函数、二次函数解析式,相似三角形的判定与性质.第(3)小题中,用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
相关题目
 (2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( )
(2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( ) (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是