��Ŀ����
����Ŀ����һ��ֱ��������ֽƬABO��������ƽ��ֱ������ϵ�У���A�� ![]() ��0������B��0��3������O��0��0��
��0������B��0��3������O��0��0��
��1������OB�ϵĶ���D����D�����B��O�غϣ���DE�AOB��AB�ڵ�E������DE�۵���ֽƬ����B��������BO�ϵĵ�F����
����ͼ����DΪOB�е�ʱ����E������ꣻ
������AF������AEFΪֱ��������ʱ����E�����ꣻ
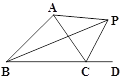
��2��P��AB���ϵĶ��㣨��P�����B�غϣ�������AOP��OP���ڵ�ֱ���۵����õ���A��OP������BA�䣬��BA��ȡ����Сֵʱ����P�����ֱ꣨��д��������ɣ���
���𰸡�
��1���⣺�١�DE��OB��OA��OB��
��DE��OA��
��DΪOB�е㣬
��DEΪ��BOA����λ�ߣ�
���EΪ�߶�A��B���е㣬
���E�������� ![]() ��
�� ![]() ����
����
�����۵���֪����BDE�ա�FDE��
���EFB=��ABO=30�㣬DF=BD��
���AEF=��ABO+��BFE=60���90�㣮
�ߡ�AEF��ֱ�������Σ�
���AFE=90����EAF=90�㣮
��i������AFE=90��ʱ����ͼ1��ʾ��
��AFO=180�㩁��AFE����EFB=60�㣮
��Rt��AOF�У���AFO=60�㣬AO= ![]() ��
��
���FAO=30�㣬AF=2OF��
�� ![]() =AO��
=AO��
��OF=1��AF=2��
��Rt��DEF�У���DFE=30�㣬DF=BD= ![]() =1��
=1��
��EF=2DE��
�� ![]() =DF=1��
=DF=1��
��DE= ![]() ��DF=
��DF= ![]() ��
��
��OD=OF+DF=2��
���E�������� ![]() ��2����
��2����
��ii������EAF=90��ʱ����ͼ2��ʾ��
�ߡ�AOB=90�㣬��ABO=30�㣬
���BAO=60�㣬
���FAO=��EAF����BAO=30�㣮
��Rt��AOF�У���FAO=30�㣬AO= ![]() ��
��
��AF=2OF��
�� ![]() =AO��
=AO��
��OF=1��AF=2��
��Rt��DEF�У���DFE=30�㣬DF= ![]() =2��
=2��
��EF=2DE��
�� ![]() =DF��
=DF��
��DE= ![]() ��
��
��OD=DF��OF=1��
���E�������� ![]() ��1����
��1����
��������������AEFΪֱ��������ʱ��E������Ϊ�� ![]() ��2����
��2���� ![]() ��1��
��1��
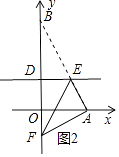
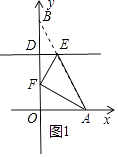
��2���⣺���۵���֪����AOP�ա�A��OP��
��OA��=OA= ![]() ����AOP=��A��OP��
����AOP=��A��OP��
�֡�OB=3��
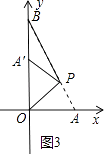
�൱��A����y����ʱ��BA��ȡ��Сֵ����ͼ3��ʾ��
�ߡ�AOB=90�㣬
���AOP=45�㣬
��ֱ��OP�Ľ���ʽΪy=x��
��ֱ��AB�Ľ���ʽΪy=kx+b��
��A�� ![]() ��0����B��0��3������y=kx+b��
��0����B��0��3������y=kx+b��
![]() ����ã�
����ã� ![]() ��
��
��ֱ��AB�Ľ���ʽΪy=�� ![]() x+3��
x+3��
����ֱ��OP��AB�Ľ���ʽ�ɷ����飬
![]() ����ã�
����ã� 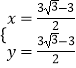 ��
��
�൱BA��ȡ����Сֵʱ��P������Ϊ�� ![]() ��
�� ![]() ����
����
����������1������DΪOB�е���DE��OA���ɵó�DEΪ��BOA����λ�ߣ��ٸ��ݵ�A��B�����꼴�ɵó���E�����ꣻ�ڸ����۵������ʽ�Ͻǵļ���ɵó���AEF=60���90�㣬�֡�AFE=90��͡�EAF=90������������ǣ����ú�30�Ƚǵ�ֱ���������Լ����ɶ������������E�����ꣻ��2�����������ε����߹�ϵ���ҳ�����A����y����ʱ��BA��ȡ��Сֵ�������۵������ʿɵó�ֱ��OP�Ľ���ʽ���ٸ��ݵ�A��B���������ô���ϵ�������ֱ��AB�Ľ���ʽ��������ֱ�߽���ʽ�ɷ����飬��֮���ɵó���P�����꣮
�����㾫����������Ĺؼ��������ⷭ�۱任���۵����⣩�����֪ʶ�������۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ��Լ������������ε�Ӧ�õ����⣬�˽��ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�