题目内容
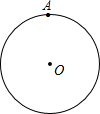 已知如图,点A是⊙O上一点.
已知如图,点A是⊙O上一点.(1)求作:⊙O的内接正△ABC;
(2)若⊙O的半径为6cm,求△ABC的面积.
分析:(1)以A为圆心,AO长为半径,把圆六等分,隔一个点取一个,可画出等边三角形;
(2)根据等边三角形的性质可得AB和DO的长,算出△ABO的面积后再计算出△ABC的面积.
(2)根据等边三角形的性质可得AB和DO的长,算出△ABO的面积后再计算出△ABC的面积.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)连接AO、BO,过O作DO⊥AB于D,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABO=30°,
∵BO=6cm,
∴DO=3cm,BD=3
cm,
∴S△ABO=
×AB×DO=
×6
×3=9
(cm2),
∴△ABC的面积为9
×3=27
(cm2).
 解:(1)如图所示;
解:(1)如图所示;(2)连接AO、BO,过O作DO⊥AB于D,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABO=30°,
∵BO=6cm,
∴DO=3cm,BD=3
| 3 |
∴S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴△ABC的面积为9
| 3 |
| 3 |
点评:此题主要考查了复杂作图,以及求圆内接三角形的面积,关键是正确画出图形,掌握圆内接正多边形的性质.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )


| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
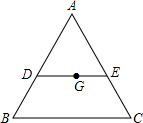 已知如图,点G是△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,那么S△ADE:S△ABC=
已知如图,点G是△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,那么S△ADE:S△ABC=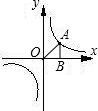 已知如图,点A是反比例函数y=
已知如图,点A是反比例函数y=
 B.
B.
 D.
D.