题目内容
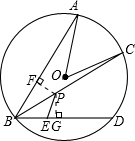
如图,A、B、C是⊙O上的三点,以BC为一边,作∠CBD=∠ABC,过BC上一点P,作PE∥AB交BD于点E.若∠AOC=60°,BE=3,则点P到弦AB的距离为______.


过P作PF⊥AB,PG⊥BD
∵∠CBD=∠ABC,PE∥AB交BD于点E,∠AOC=60°,BE=3
∴∠CBD=∠ABC=30°
∵BC为∠ABD的角平分线,PF=PG
又∵PE∥AB
∴∠BPE=∠ABC=∠CBD=30°
∴∠PEG=∠BPE+∠CBD=30°+30°=60°
∵PG⊥BD
∴∠PGE=90°
∴sin∠PEG=
即
=
∴PG=
×PE=
×3=
,
∴则点P到弦AB的距离为PF=PG=
,
故答案为:
.
∵∠CBD=∠ABC,PE∥AB交BD于点E,∠AOC=60°,BE=3
∴∠CBD=∠ABC=30°
∵BC为∠ABD的角平分线,PF=PG
又∵PE∥AB
∴∠BPE=∠ABC=∠CBD=30°
∴∠PEG=∠BPE+∠CBD=30°+30°=60°
∵PG⊥BD
∴∠PGE=90°
∴sin∠PEG=
| PG |
| PE |
即
| PG |
| PE |
| ||
| 2 |
∴PG=
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴则点P到弦AB的距离为PF=PG=
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |


练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目


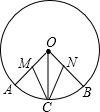
 α(0°<α<90°),此时量角器的半圆弧与EF相交于点P,设点P处量角器的读数为n°.
α(0°<α<90°),此时量角器的半圆弧与EF相交于点P,设点P处量角器的读数为n°.

