ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµČŃüRt”÷ABCÖŠ£¬”ĻC=90”ć£¬AC=8£¬FŹĒAB±ßÉĻµÄÖŠµć£¬µćD£¬E·Ö±šŌŚAC£¬BC±ßÉĻŌĖ¶Æ£¬ĒŅ±£³ÖAD=CE£®Į¬½ÓDE£¬DF£¬EF£®ŌŚ“ĖŌĖ¶Æ±ä»ÆµÄ¹ż³ĢÖŠ£¬ĻĀĮŠ½įĀŪ£ŗ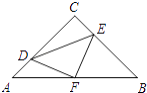
¢Ł”÷DFEŹĒµČŃüÖ±½ĒČż½ĒŠĪ£»
¢ŚĖıߊĪCDFE²»æÉÄÜĪŖÕż·½ŠĪ£¬
¢ŪDE³¤¶ČµÄ×īŠ”ÖµĪŖ4£»
¢ÜĖıߊĪCDFEµÄĆ껿±£³Ö²»±ä£»
¢Ż”÷CDEĆ껿µÄ×ī“óÖµĪŖ8£®
ĘäÖŠÕżČ·µÄ½įĀŪŹĒ£Ø £©
A.¢Ł¢Ś¢Ū
B.¢Ł¢Ü¢Ż
C.¢Ł¢Ū¢Ü
D.¢Ū¢Ü¢Ż
”¾“š°ø”æB
”¾½āĪö”æ½ā£ŗĮ¬½ÓCF£»
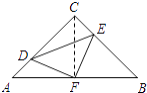
”ß”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻFCB=”ĻA=45”ć£¬CF=AF=FB£»
”ßAD=CE£¬
”ą”÷ADF”Õ”÷CEF£ØSAS£©£»
”ąEF=DF£¬”ĻCFE=”ĻAFD£»
”ß”ĻAFD+”ĻCFD=90”ć£¬
”ą”ĻCFE+”ĻCFD=”ĻEFD=90”ć£¬
”ą”÷EDFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£Ø¹Ź¢ŁÕżČ·£©£®
µ±D”¢E·Ö±šĪŖAC”¢BCÖŠµćŹ±£¬ĖıߊĪCDFEŹĒÕż·½ŠĪ£Ø¹Ź¢Ś“ķĪ󣩣®
”ß”÷ADF”Õ”÷CEF£¬
”ąS”÷CEF=S”÷ADF
”ąSĖıߊĪCEFD=S”÷AFC£¬£Ø¹Ź¢ÜÕżČ·£©£®
ÓÉÓŚ”÷DEFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬Ņņ“Ėµ±DE×īŠ”Ź±£¬DFŅ²×īŠ”£»
¼“µ±DF”ĶACŹ±£¬DE×īŠ”£¬“ĖŹ±DF= ![]() BC=4£®
BC=4£®
”ąDE= ![]() DF=4
DF=4 ![]() £Ø¹Ź¢Ū“ķĪ󣩣®
£Ø¹Ź¢Ū“ķĪ󣩣®
µ±”÷CDEĆ껿×ī“óŹ±£¬ÓÉ¢ÜÖŖ£¬“ĖŹ±”÷DEFµÄĆ껿×īŠ”£®
“ĖŹ±S”÷CDE=SĖıߊĪCEFD©S”÷DEF=S”÷AFC©S”÷DEF=16©8=8£Ø¹Ź¢ŻÕżČ·£©£®
¹ŹB·ūŗĻĢāŅā.
¹Ź“š°øĪŖ£ŗB£®
Į¬½ÓCF.ĻČÖ¤Ć÷”÷ADF”Õ”÷CEFæɵĆEF=DF”¢”ĻCFE=”ĻAFD£¬ŌŁÓÉ”ĻAFD+”ĻCFD=90”ćæɵƔĻEFD=90”ć£¬“Ó¶ųÅŠ¶Ļ¢Ł£»
µ±D”¢E·Ö±šĪŖAC”¢BCÖŠµćŹ±£¬ĖıߊĪCDFEŹĒÕż·½ŠĪ£¬“Ó¶ųÅŠ¶Ļ¢Ś£»
ÓÉÓŚ”÷DEFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬Ņņ“Ėµ±DE×īŠ”Ź±£¬DFŅ²×īŠ”£¬¼“µ±DF”ĶACŹ±£¬DE×īŠ”£¬“Ó¶ųĒó³öDFµÄÖµ£¬½ų¶ųæɵĆDEµÄÖµ£¬æÉÅŠ¶Ļ¢Ū£»
ÓÉ”÷ADF”Õ”÷CEFæɵĆSĖıߊĪCEFD=S”÷AFC£¬“Ó¶ųÅŠ¶Ļ¢Ü£»
ÓÉ¢ÜÖŖ£¬“ĖŹ±”÷DEFµÄĆ껿×īŠ”£®“ĖŹ±S”÷CDE=SĖıߊĪCEFD©S”÷DEF=S”÷AFC©S”÷DEF£¬“Ó¶ųĒó³ö”÷CDEµÄĆ껿£¬æÉÅŠ¶Ļ¢Ż.

 Ķ¬²½Į·Ļ°ŗÓÄĻ“óѧ³ö°ęÉēĻµĮŠ“š°ø
Ķ¬²½Į·Ļ°ŗÓÄĻ“óѧ³ö°ęÉēĻµĮŠ“š°ø Ķ¬²½Į·Ļ°Ī÷ÄĻŹ¦·¶“óѧ³ö°ęÉēĻµĮŠ“š°ø
Ķ¬²½Į·Ļ°Ī÷ÄĻŹ¦·¶“óѧ³ö°ęÉēĻµĮŠ“š°ø ²¹³äĻ°Ģā½ĖÕĻµĮŠ“š°ø
²¹³äĻ°Ģā½ĖÕĻµĮŠ“š°ø