题目内容
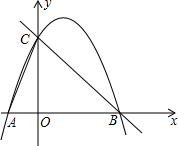
如图1,点A是直线y=kx(k>0,且k为常数)上一动点,以A为顶点的抛物线y=(x-h)2+m交直线y=kx于另一点E,交y轴于点F,抛物线的对称轴交x轴于点B,交直线EF于点C.(点A,E,F两两不重合)
(1)请写出h与m之间的关系;(用含的k式子表示)
(2)当点A运动到使EF与x轴平行时(如图2),求线段AC与OF的比值;
(3)当点A运动到使点F的位置最低时(如图3),求线段AC与OF的比值.

(1)请写出h与m之间的关系;(用含的k式子表示)
(2)当点A运动到使EF与x轴平行时(如图2),求线段AC与OF的比值;
(3)当点A运动到使点F的位置最低时(如图3),求线段AC与OF的比值.

(1)∵抛物线顶点(h,m)在直线y=kx上,
∴m=kh;
(2)方法一:解方程组
,
将(2)代入(1)得到:(x-h)2+kh=kx,
整理得:(x-h)[(x-h)-k]=0,
解得:x1=h,x2=k+h,
代入到方程(2)y1=hy2=k2+hk,
所以点E坐标是(k+h,k2+hk),
当x=0时,y=(x-h)2+m=h2+kh,
∴点F坐标是(0,h2+kh),
当EF和x轴平行时,点E,F的纵坐标相等,
即k2+kh=h2+kh,
解得:h=k(h=-k舍去,否则E,F,O重合),
此时点E(2k,2k2),F(0,2k2),C(k,2k2),A(k,k2),
∴AC:OF=k2:2k2=1:2.(3分)
方法二:当x=0时,y=(x-h)2+m=h2+kh,即F(0,h2+kh),
当EF和x轴平行时,点E,F的纵坐标相等,
即点E的纵坐标为h2+kh,
当y=h2+kh时,代入y=(x-h)2+kh,
解得x=2h(0舍去,否则E,F,O重合),
即点E坐标为(2h,h2+kh),(1分)
将此点横纵坐标代入y=kx得到h=k(h=0舍去,否则点E,F,O重合),
此时点E(2k,2k2),F(0,2k2),C(k,2k2),A(k,k2),
∴AC:OF=k2:2k2=1:2.
方法三:∵EF与x轴平行,
根据抛物线对称性得到FC=EC,
∵AC∥FO,
∴∠ECA=∠EFO,∠FOE=∠CAE,
∴△OFE∽△ACE,
∴AC:OF=EC:EF=1:2.
(3)当点F的位置处于最低时,其纵坐标h2+kh最小,
∵h2+kh=[h2+kh+(
)2]-
,
当h=-
,点F的位置最低,此时F(0,-
),
解方程组
得E(
,
),A(-
,-
).
方法一:设直线EF的解析式为y=px+q,
将点E(
,
),F(0,-
)的横纵坐标分别代入得
,
解得:p=
k,q=-
k2,
∴直线EF的解析式为y=
kx-
k2,
当x=-
时,y=-k2,即点C的坐标为(-
,-k2),
∵点A(-
k,-
),
∴AC=
,而OF=
k2,
∴AC=2OF,即AC:OF=2.
方法二:∵E(
,
),A(-
,-
),
∴点A,E关于点O对称,
∴AO=OE,
∵AC∥FO,
∴∠ECA=∠EFO,∠FOE=∠CAE,
∴△OFE∽△ACE,
∴AC:OF=AE:OE=2:1.
∴m=kh;
(2)方法一:解方程组
|
将(2)代入(1)得到:(x-h)2+kh=kx,
整理得:(x-h)[(x-h)-k]=0,
解得:x1=h,x2=k+h,
代入到方程(2)y1=hy2=k2+hk,
所以点E坐标是(k+h,k2+hk),
当x=0时,y=(x-h)2+m=h2+kh,
∴点F坐标是(0,h2+kh),
当EF和x轴平行时,点E,F的纵坐标相等,
即k2+kh=h2+kh,
解得:h=k(h=-k舍去,否则E,F,O重合),
此时点E(2k,2k2),F(0,2k2),C(k,2k2),A(k,k2),
∴AC:OF=k2:2k2=1:2.(3分)
方法二:当x=0时,y=(x-h)2+m=h2+kh,即F(0,h2+kh),
当EF和x轴平行时,点E,F的纵坐标相等,
即点E的纵坐标为h2+kh,
当y=h2+kh时,代入y=(x-h)2+kh,
解得x=2h(0舍去,否则E,F,O重合),
即点E坐标为(2h,h2+kh),(1分)
将此点横纵坐标代入y=kx得到h=k(h=0舍去,否则点E,F,O重合),
此时点E(2k,2k2),F(0,2k2),C(k,2k2),A(k,k2),
∴AC:OF=k2:2k2=1:2.
方法三:∵EF与x轴平行,
根据抛物线对称性得到FC=EC,
∵AC∥FO,
∴∠ECA=∠EFO,∠FOE=∠CAE,
∴△OFE∽△ACE,
∴AC:OF=EC:EF=1:2.
(3)当点F的位置处于最低时,其纵坐标h2+kh最小,
∵h2+kh=[h2+kh+(
| k |
| 2 |
| k2 |
| 4 |
当h=-
| k |
| 2 |
| k2 |
| 4 |
解方程组
|
得E(
| k |
| 2 |
| k2 |
| 2 |
| k |
| 2 |
| k2 |
| 2 |
方法一:设直线EF的解析式为y=px+q,
将点E(
| k |
| 2 |
| k2 |
| 2 |
| k2 |
| 4 |
|
解得:p=
| 3 |
| 2 |
| 1 |
| 4 |
∴直线EF的解析式为y=
| 3 |
| 2 |
| 1 |
| 4 |
当x=-
| k |
| 2 |
| k |
| 2 |
∵点A(-
| 1 |
| 2 |
| k2 |
| 2 |
∴AC=
| k2 |
| 2 |
| 1 |
| 4 |
∴AC=2OF,即AC:OF=2.
方法二:∵E(
| k |
| 2 |
| k2 |
| 2 |
| k |
| 2 |
| k2 |
| 2 |
∴点A,E关于点O对称,
∴AO=OE,
∵AC∥FO,
∴∠ECA=∠EFO,∠FOE=∠CAE,
∴△OFE∽△ACE,
∴AC:OF=AE:OE=2:1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴的另一个交点.
轴的另一个交点. 
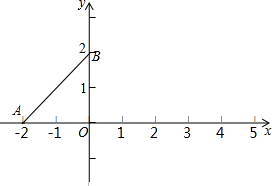 OC,(点A旋转到点B的位置),抛物线y=ax2+bx+c(a≠0)经过B,C两点,与x轴的另一个交点为点D,顶点为点P,对称轴为直线x=3,
OC,(点A旋转到点B的位置),抛物线y=ax2+bx+c(a≠0)经过B,C两点,与x轴的另一个交点为点D,顶点为点P,对称轴为直线x=3, B运动;同时,点N从B点出发沿折线段BC-CO以每秒1个单位长的速度向终点O运动、设运动时间为t秒.
B运动;同时,点N从B点出发沿折线段BC-CO以每秒1个单位长的速度向终点O运动、设运动时间为t秒.
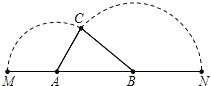 点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.