题目内容
【题目】如图，直线y=x－2与y轴交于点C，与x轴交于点B，与反比例函数
的图象在第一象限交于点A，连接OA，若S△AOB
S△BOC = 1:2，则k的值为（ ）
A．2 B．3 C．4 D．6
【答案】B．
【解析】
试题分析：过A作AD⊥ｙ轴，AE⊥x轴，由S△AOB
S△BOC = 1:2可得AD：OB=3：2，从而可求AD=3，代入直线解析式可求AE=1，进而确定k=3．
试题解析：如图，过A作AD⊥ｙ轴，AE⊥x轴，
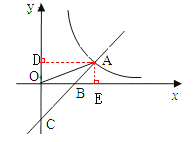
∵S△AOBS△BOC = 1:2
∴S△AOCS△BOC = 3:2
∴AD：OB=3：2
令y=0，即x-2=0
∴x=2,即AD=3，
把AD=3代入y=x-2,得y=1,即AE=1；
∴k=AD×AE=3×1=3．
故选B．
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
⑴ac＜0；
⑵当x＞1时，y的值随x值的增大而减小．
⑶3是方程ax2+（b﹣1）x+c=0的一个根；
⑷当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（）
A. 4个 B. 3个 C. 2个 D. 1个