题目内容
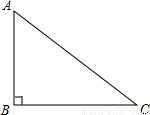
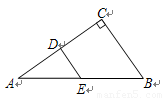
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.(1)请画出这个直角三角形的内切圆;
(2)并求出此内切圆的半径.
【答案】分析:(1)先作出任意两个角的角平分线,再以角平分线交点为圆心,以交点与任意一边的距离为半径画圆即可;
(2)利用勾股定理和三角形的面积公式来确定内切圆的半径.
解答: 解:(1)作图:
解:(1)作图:
(2)如图,连接OA、OB、OC、OD、OE、OF.
在Rt△ABC中,
设AB=x,则BC=x+1.
∵AC=5,
∴x2+(x+1)2=25,
∴x1=3,x2=-4.(舍)
∴AB=3,BC=4.
设内切圆半径=R.
∵S△ABC= ×3×4=6.
×3×4=6.
∴S△ABC=S△AOB+S△BOC+S△AOC
= ×AB×R+
×AB×R+ ×BC×R+
×BC×R+ ×AC×R
×AC×R
=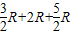
=6R.
∴6R=6,
∴内切圆的半径为1.
点评:外心是三角形各边垂直平分线的交点,到每个顶点的距离相等.内心是三角形每个角的角平分线的交点,到三边距离相等.
(2)利用勾股定理和三角形的面积公式来确定内切圆的半径.
解答:
 解:(1)作图:
解:(1)作图:(2)如图,连接OA、OB、OC、OD、OE、OF.
在Rt△ABC中,
设AB=x,则BC=x+1.
∵AC=5,
∴x2+(x+1)2=25,
∴x1=3,x2=-4.(舍)
∴AB=3,BC=4.
设内切圆半径=R.
∵S△ABC=
 ×3×4=6.
×3×4=6.∴S△ABC=S△AOB+S△BOC+S△AOC
=
 ×AB×R+
×AB×R+ ×BC×R+
×BC×R+ ×AC×R
×AC×R=
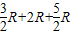
=6R.
∴6R=6,
∴内切圆的半径为1.
点评:外心是三角形各边垂直平分线的交点,到每个顶点的距离相等.内心是三角形每个角的角平分线的交点,到三边距离相等.

练习册系列答案
相关题目
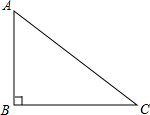 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5. 中(∠
中(∠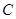 =90o),放置边长分别3,4,
=90o),放置边长分别3,4, 的三个正方形,
的三个正方形,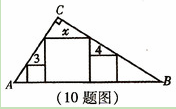
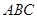 中,
中, ,
,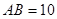 ,
,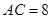 ,点
,点 、
、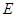 分别为
分别为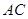 和
和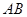 的中点,则
的中点,则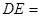 ( ).
( ).
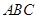 中,斜边
中,斜边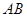 的长为
的长为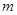 ,
, ,则直角边
,则直角边 的长是( )
的长是( )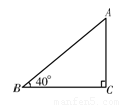
 B.
B.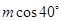
 D.
D.