题目内容
(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.

(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.

分析:(1)根据正方形的性质和等腰直角三角形的性质就可以求得△ADP与△ABQ全等;
(2)根据正方形的性质和等腰直角三角形的性质就可以得△ANO≌△BMO,从而得出ON=OM;
(3)过点O作OE⊥AB于E,O H⊥BC于H,由条件求出OE、OH的值,再通过证明△OEN∽△OHM,利用相似三角形的性质就可以求出结论.
(2)根据正方形的性质和等腰直角三角形的性质就可以得△ANO≌△BMO,从而得出ON=OM;
(3)过点O作OE⊥AB于E,O H⊥BC于H,由条件求出OE、OH的值,再通过证明△OEN∽△OHM,利用相似三角形的性质就可以求出结论.
解答:解:(1)△ADP≌△ABQ.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
,
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
,
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,过点O作OE⊥AB于E,O H⊥BC于H,
∴∠OEN=∠OHM=90°,OE=
AD,OH=
AB.
∵AB=4,AD=6,
∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴
=
.
∵OM=x,ON=y,
∴
=
,
∴y=
x.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
|
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
|
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,过点O作OE⊥AB于E,O H⊥BC于H,
∴∠OEN=∠OHM=90°,OE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=4,AD=6,

∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴
| OE |
| OH |
| ON |
| OM |
∵OM=x,ON=y,
∴
| 3 |
| 2 |
| y |
| x |
∴y=
| 3 |
| 2 |
点评:本题考查了全等三角形的判定及性质的运用,正方形的性质、等腰直角三角形的性质的运用,相似三角形的判定及性质的运用,在求函数的解析式时证明三角形相似是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
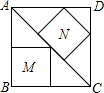 把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是
把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是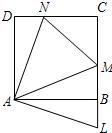 20、如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,使得△CMN的周长为2,将△AND绕点A顺时针旋转90°得△ABL,求证:△ANM≌△ALM.
20、如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,使得△CMN的周长为2,将△AND绕点A顺时针旋转90°得△ABL,求证:△ANM≌△ALM.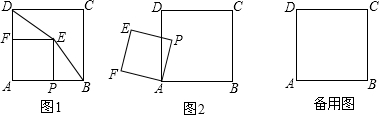
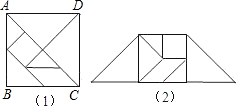 七巧板是我们祖先创造的一种智力玩具,它来源于勾股法,如图(1)整幅七巧板是由正方形ABCD分割成大小七块(其中五块是等腰三角形,一块是正方形和一块平行四边形)组成,如图(2)是由七巧板拼成一个梯形,如果正方形ABCD的边长为2
七巧板是我们祖先创造的一种智力玩具,它来源于勾股法,如图(1)整幅七巧板是由正方形ABCD分割成大小七块(其中五块是等腰三角形,一块是正方形和一块平行四边形)组成,如图(2)是由七巧板拼成一个梯形,如果正方形ABCD的边长为2 20、如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为
20、如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为