题目内容
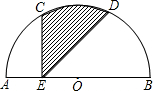 如图所示,AB为半圆的直径,C、D为弧
如图所示,AB为半圆的直径,C、D为弧 | AB |
分析:连OC、OD、CD,根据弧相等则弧所对的圆心角相等得到∠AOC=∠COD=∠BOD=
×180°=60°,则△OCD为等边三角形,即有∠OCD=60°,所以CD∥AB,于是得到S△ECD=S△OCD,可把求阴影部分的面积的问题转化为求扇形OCD的面积,然后根据扇形的面积公式计算即可.
| 1 |
| 3 |
解答: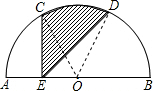 解:连OC、OD、CD,如图,
解:连OC、OD、CD,如图,
∵AB为半圆的直径,C、D为弧
的三等分点,
∴∠AOC=∠COD=∠BOD=
×180°=60°,
而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△ECD=S△OCD,
∴阴影部分的面积=S扇形OCD=
=
πR2.
故答案为:
πR2.
 解:连OC、OD、CD,如图,
解:连OC、OD、CD,如图,∵AB为半圆的直径,C、D为弧
 |
| AB |
∴∠AOC=∠COD=∠BOD=
| 1 |
| 3 |
而OC=OD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴CD∥AB,
∴S△ECD=S△OCD,
∴阴影部分的面积=S扇形OCD=
| 60•π•R2 |
| 360 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题考查了扇形的面积公式:S=
(n为扇形的圆心角的度数,R为圆的半径).也考查了弧与圆心角之间的关系以及等边三角形的性质.
| n•π•R2 |
| 360 |

练习册系列答案
相关题目
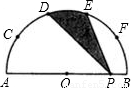
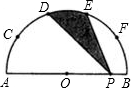 如图所示,AB为半圆O的直径,C、D、E、F是
如图所示,AB为半圆O的直径,C、D、E、F是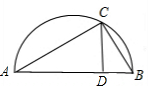 如图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD:DB=3:2,则AC•BC等于
如图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD:DB=3:2,则AC•BC等于 如图所示,AB为半圆的直径,C为半圆上一点,且
如图所示,AB为半圆的直径,C为半圆上一点,且 上的五等分点,P为直径AB上的任意一点,若AB=4,则图中阴影部分的面积为 .
上的五等分点,P为直径AB上的任意一点,若AB=4,则图中阴影部分的面积为 .