题目内容
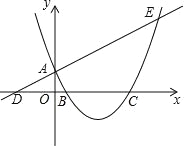
【题目】(本小题满分9分)等边△ABC的边长为2,P是BC边上的一动点(不与B,C重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB,AC交于点M,N. (如图1).
(1)求证:AM=AN;
(2)若BM=![]() ,求x的值;
,求x的值;
(3)求四边形ADPE与△ABC重叠部分的面积S与x之间的函数关系式及S的最小值;
(4)如图2,连接DE分别与边AB,AC交于点G,H.当x为何值时,∠BAD=15 .

【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)S
;(3)S![]() (x﹣1)2+
(x﹣1)2+![]() ,S的最小值为
,S的最小值为![]() ;(4)x=2
;(4)x=2![]() ﹣2
﹣2
【解析】
试题分析:(1)根据等边三角形的性质得到∠PAN=∠DAM,证明△ADM≌△APN,根据全等三角形的性质证明结论;
(2)证明△BPM∽△CAP,根据相似三角形的性质列出比例式,解方程即可;
(3)作PH⊥AB于H,根据勾股定理和锐角三角函数的概念求出S△ADP,根据四边形ADPE与△ABC重叠部分四边形AMPN的面积S=△ADP的面积得到答案;
(4)连接PG,根据菱形的性质、等腰直角三角形的性质计算即可.
试题解析:(1)∵△ABC、△APD、△APE都是等边三角形,
∴AD=AP,∠ADM=∠APN=60°,∠DAP=∠BAC=60°,
∴∠PAN=∠DAM,
在△ADM和△APN中,
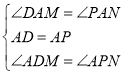 ,
,
∴△ADM≌△APN,
∴AM=AN;
(2)∵∠PMB=∠MPA+∠BAP,∠APC=∠B+∠BAP,∠MPA=∠B=60°,
∴∠PMB=∠APC,又∠B=∠C,
∴△BPM∽△CAP,
∴![]() ,即
,即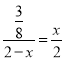 ,
,
整理得,4x2﹣8x+3=0,
解得,x1=![]() ,x2=
,x2=![]() ,
,
∴当BM=![]() 时,x的值为
时,x的值为![]() 或
或![]() ;
;
(3)如图1,作PH⊥AB于H,
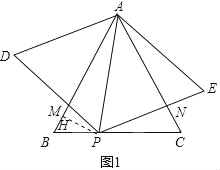
∵△ADM≌△APN,
∴四边形ADPE与△ABC重叠部分四边形AMPN的面积S=△ADP的面积,
∵BP=x,∠B=60°,
∴BH=![]() x,PH=
x,PH=![]() x,
x,
∴AH=2﹣![]() x,
x,
由勾股定理得,AP2=AH2+PH2=(2﹣![]() x)2+(
x)2+(![]() x)2=x2﹣2x+4,
x)2=x2﹣2x+4,
∵△ADP是等边三角形,
∴S△ADP=![]() ×
×![]() AP×AP=
AP×AP=![]() AP2=
AP2=![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴S的最小值为![]() ;
;
(4)连接PG,
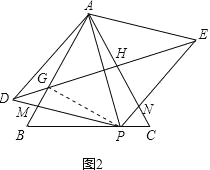
当∠BAD=15°时,∵∠DAP=60°,
∴∠GAP=45°,
∵四边形ADPE是菱形,
∴AP⊥DE,
∴AG=PG,
∵∠B=60°,BP=x,
∴BG=![]() x,AG=PG=
x,AG=PG=![]() x,
x,
∴![]() x+
x+![]() x=2,
x=2,
解得,x=2![]() ﹣2,
﹣2,
∴当x=2![]() ﹣2时,∠BAD=15°.
﹣2时,∠BAD=15°.