��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2-2ax-3a��a��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��y=kx+b��y�ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��1��ֱ��д����A�����꣬����ֱ��l�ĺ�������ʽ������k��b�ú�a��ʽ�ӱ�ʾ����
��2����E��ֱ��l�Ϸ����������ϵ�һ�㣬����ACE����������ֵΪ![]() ����a��ֵ��
����a��ֵ��
��3����P�������߶Գ����ϵ�һ�㣬��Q���������ϣ��Ե�A��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��A��-1��0����y=ax+a����2��a=-![]() ����3��P�������ΪP1��1��-4����P2��1��-
����3��P�������ΪP1��1��-4����P2��1��-![]() ����
����
��������
�����������1����������y=ax2-2ax-3a��a��0����x�ύ������A��B�����A������꣬��DF��x����F������ƽ���߷��߶γɱ����������D�����꣬Ȼ�����ô���ϵ�������������ֱ��l�ĺ�������ʽ��
��2�����E��m��a��m+1����m-3������yAE=k1x+b1�����ô���ϵ����ȷ��yAE=a��m-3��x+a��m-3�����Ӷ�ȷ��S��ACE=![]() ��m+1��[a��m-3��-a]=
��m+1��[a��m-3��-a]=![]() ��m-
��m-![]() ��2-
��2-![]() a��������ֵȷ��a��ֵ���ɣ�
a��������ֵȷ��a��ֵ���ɣ�
��3������ADΪ�Խ��ߡ���ACΪ�ߣ�APΪ�Խ��ߡ���ACΪ�ߣ�AQΪ�Խ�������������þ��ε�����ȷ����P�����꼴�ɣ�
�����������1����y=0����ax2-2ax-3a=0��
���x1=-1��x2=3
�ߵ�A�ڵ�B����࣬
��A��-1��0����
��ͼ1����DF��x����F��
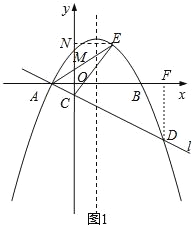
��DF��OC��
��![]() ��
��
��CD=4AC��
��![]() =4��
=4��
��OA=1��
��OF=4��
��D��ĺ�����Ϊ4��
����y=ax2-2ax-3a�ã�y=5a��
��D��4��5a����
��A��D�������y=kx+b��![]() ��
��
���![]() ��
��
��ֱ��l�ĺ�������ʽΪy=ax+a��
��2����ͼ1������E��EN��y���ڵ�N
���E��m��a��m+1����m-3������yAE=k1x+b1��
��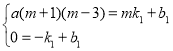 ��
��
��ã�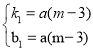 ��
��
��yAE=a��m-3��x+a��m-3����M��0��a��m-3����
��MC=a��m-3��-a��NE=m
��S��ACE=S��ACM+S��CEM=![]() [a��m-3��-a]+
[a��m-3��-a]+ ![]() [a��m-3��-a]m
[a��m-3��-a]m
=![]() ��m+1��[a��m-3��-a]
��m+1��[a��m-3��-a]
= ![]() ��m-
��m-![]() ��2-
��2-![]() a��
a��
�������ֵ-![]() a=
a=![]() ��
��
��a=-![]() ��
��
��3����ax2-2ax-3a=ax+a����ax2-3ax-4a=0��
���x1=-1��x2=4��
��D��4��5a����
��y=ax2-2ax-3a��
�������ߵĶԳ���Ϊx=1��
��P1��1��m����
����AD�Ǿ��ε�һ���ߣ�
��AQ��DP֪xD-xP=xA-xQ����֪Q�������Ϊ-4����x=-4���������߷��̵�Q��-4��21a����
m=yD+yQ=21a+5a=26a����P��1��26a����
���ı���ADPQΪ���Σ����ADP=90�㣬
��AD2+PD2=AP2��
��AD2=[4-��-1��]2+��5a��2=52+��5a��2��
PD2=[4-��-1��]2+��5a��2=52+��5a��2��
��[4-��-1��]2+��5a��2+��1-4��2+��26a-5a��2=��-1-1��2+��26a��2��
��a2=![]() ����a��0����a=-
����a��0����a=-![]() ��
��
��P1��1��-![]() ����
����
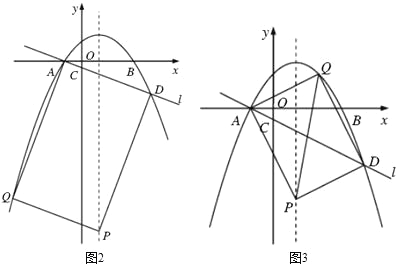
����AD�Ǿ��ε�һ���Խ��ߣ�
���߶�AD���е�����Ϊ��![]() ��
��![]() ����Q��2��-3a����
����Q��2��-3a����
m=5a-��-3a��=8a����P��1��8a����
���ı���ADPQΪ���Σ����APD=90�㣬
��AP2+PD2=AD2��
��AP2=[1-��-1��]2+��8a��2=22+��8a��2��
PD2=��4-1��2+��8a-5a��2=32+��3a��2��
AD2=[4-��-1��]2+��5a��2=52+��5a��2��
��22+��8a��2+32+��3a��2=52+��5a��2��
���a2=![]() ����a��0����a=-
����a��0����a=-![]() ��
��
��P2��1��-4����
���Ͽɵã�P�������ΪP1��1��-4����P2��1��-![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
