题目内容
(2013•宜春模拟)课题:探求直角梯形剪开后进行旋转、平移操作相关问题.如图1,小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=10,AD=8.在进行如下操作时遇到了下面的几个问题,请你帮助解决.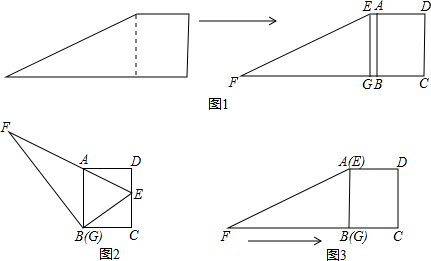
观察计算:
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2),请你求出AE和FG的长度.
探索发现:
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为20时,平移距离x的值(如图3).
(3)在(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).

观察计算:
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2),请你求出AE和FG的长度.
探索发现:
(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为20时,平移距离x的值(如图3).
(3)在(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).
分析:(1)利用矩形的性质以及得出△BEM∽△FEB,求出即可;
(2)有两种情况:①当0≤x≤8时,根据平行线分线段成比例定理求出BM的值,根据梯形的面积公式求出即可;②当8≤x≤20时,求出BM、CN的值,根据梯形的面积公式求出即可;把y=20代入解析式求x即可;
(3)当16≤y<64时,平移的距离不等,两纸片重叠的面积可能相等,0≤y<16或y=64时,平移的距离不等,两纸片重叠部分的面积也不可能相等.
(2)有两种情况:①当0≤x≤8时,根据平行线分线段成比例定理求出BM的值,根据梯形的面积公式求出即可;②当8≤x≤20时,求出BM、CN的值,根据梯形的面积公式求出即可;把y=20代入解析式求x即可;
(3)当16≤y<64时,平移的距离不等,两纸片重叠的面积可能相等,0≤y<16或y=64时,平移的距离不等,两纸片重叠部分的面积也不可能相等.
解答: 解:(1)如答题图1,过B作BM⊥AE于M.
解:(1)如答题图1,过B作BM⊥AE于M.
由AB=BE=10,BC=8,
∴CE=6.
∴DE=4.
∴AE=4
.
由AB=BE,BM⊥AE,
∴EM=2
.
∴BM=4
.
由△BEM∽△FEB,
∴
=
,
∴FG=20.
(2)①
如答题图2:∵矩形ABCD,∠EGF=90°,EG=AB,
∴AB∥CD∥EG,
∴
=
,
即
=
,
∴BM=10-
x,
∴y=
(BM+EG)×BG=
•(10-
x+10)•x,
∴y=-
x2+10x(0≤x≤8);
②如图2:与求BM的方法类似,得出
=
,
∴CN=14-
x,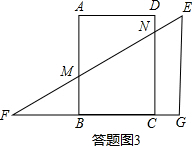
∴y=
(BM+CN)×BC=
•(10-
x+14-
x)•8=-4x+96(8<x≤20);
综合上述:y与x的关系式是y=
,
把y=20代入y=-
x2+10x得:-
x2+10x=20,
解得:x1=20+8
>8(舍去),x2=20-8
;
把y=20代入y=-4x+96得:-4x+96=20,
解得:x=19,
综上所述:当y=20时,x=20-8
或x=19;
(3)当0≤x≤8时,
y=-
x2+10x=-
(x-20)2+100,
顶点为(20,100),
∴当0≤x≤8时,0≤y≤64.
当8<x≤20时,y=-4x+96,16≤y<64.
∴当16≤y<64时,平移的距离不等,两纸片重叠的面积y可能相等.
当0≤y<16或y=64时,平移的距离不等,两纸片重叠部分的面积也不可能相等.
 解:(1)如答题图1,过B作BM⊥AE于M.
解:(1)如答题图1,过B作BM⊥AE于M.由AB=BE=10,BC=8,
∴CE=6.
∴DE=4.
∴AE=4
| 5 |
由AB=BE,BM⊥AE,
∴EM=2
| 5 |
∴BM=4
| 5 |
由△BEM∽△FEB,
∴
| FG |
| BE |
| BM |
| EM |
∴FG=20.
(2)①

如答题图2:∵矩形ABCD,∠EGF=90°,EG=AB,
∴AB∥CD∥EG,
∴
| BM |
| EG |
| FB |
| FG |
即
| BM |
| 10 |
| 20-x |
| 20 |
∴BM=10-
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴y=-
| 1 |
| 4 |
②如图2:与求BM的方法类似,得出
| CN |
| 10 |
| 20-(x-8) |
| 20 |
∴CN=14-
| 1 |
| 2 |

∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综合上述:y与x的关系式是y=
|
把y=20代入y=-
| 1 |
| 4 |
| 1 |
| 4 |
解得:x1=20+8
| 5 |
| 5 |
把y=20代入y=-4x+96得:-4x+96=20,
解得:x=19,
综上所述:当y=20时,x=20-8
| 5 |
(3)当0≤x≤8时,
y=-
| 1 |
| 4 |
| 1 |
| 4 |
顶点为(20,100),
∴当0≤x≤8时,0≤y≤64.
当8<x≤20时,y=-4x+96,16≤y<64.
∴当16≤y<64时,平移的距离不等,两纸片重叠的面积y可能相等.
当0≤y<16或y=64时,平移的距离不等,两纸片重叠部分的面积也不可能相等.
点评:此题主要考查了几何变换综合题,本题以动态(平移和旋转)的形式考查了分类讨论的思想、函数的知识和直角三角形,具有很强的综合性.

练习册系列答案
相关题目
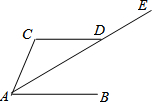 (2013•宜春模拟)如图所示,已知AE平分∠BAC交CD于点D,且AB∥CD,∠C=100°,则∠EAC为( )
(2013•宜春模拟)如图所示,已知AE平分∠BAC交CD于点D,且AB∥CD,∠C=100°,则∠EAC为( )