题目内容
【题目】如图，△DEF是△ABC经过某种变换得到的图形，点A与点D，点B与点E，
点C与点F分别是对应点，观察点与点的坐标之间的关系，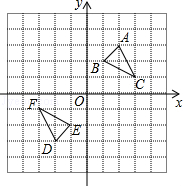
解答下列问题：
（1）分别写出点A与点D，点B与点E，点C与点F的坐标，并说说对应点的坐标有哪些特征；
（2）若点P（a+3，4﹣b）与点Q（2a，2b﹣3）也是通过上述变换得到的对应点，求a，b的值．
（3）求图中△ABC的面积．
【答案】
（1）
解：A（2，3）与D（﹣2，﹣3）；B（1，2）与E（﹣1，﹣2）；C（3，1）与F（﹣3，﹣1）．
对应点的坐标的特征：横坐标互为相反数，纵坐标互为相反数
（2）
解：由（1）可得a+3=﹣2a，4﹣b=﹣（2b﹣3）．解得a=﹣1，b=﹣1
（3）
解：三角形ABC的面积=2×2﹣ 
×2×1﹣ ×2×1﹣ ×1×1= 
【解析】（1）根据图形即可直接写出坐标；（2）根据（1）中得到的横纵坐标之间的关系可以列方程求解；（3）转化为图形的面积的和、差即可求解．
【考点精析】根据题目的已知条件，利用作轴对称图形的相关知识可以得到问题的答案，需要掌握画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
