题目内容
 如图,在正方形ABCD中,E为正方形ABCD内一点,且∠AEB=90°,tan∠BAE=
如图,在正方形ABCD中,E为正方形ABCD内一点,且∠AEB=90°,tan∠BAE=| 1 |
| 2 |
①△BEF为等腰直角三角形;②S正方形ABCD=8S△ECG;③∠ECB=∠CAG;④CG=AD.
其中正确结论的个数是( )
分析:①根据旋转的性质知,△ABE≌△CBF,由全等三角形的对应边相等证得结论;
②作辅助线AH构建正方形EHFB,然后结合已知条件“∠AEB=90°,tan∠BAE=
”求得正方形ABCD的边长与△CGE的边长间的数量关系,从而求得正方形ABCD与△CEG的面积间的数量关系;
③根据正方形的对角线平分对角以及三角形外角定理证得结论;
④将CG、BC的长度转化为与线段BE的长度的关系,然后比较它们的长短.
②作辅助线AH构建正方形EHFB,然后结合已知条件“∠AEB=90°,tan∠BAE=
| 1 |
| 2 |
③根据正方形的对角线平分对角以及三角形外角定理证得结论;
④将CG、BC的长度转化为与线段BE的长度的关系,然后比较它们的长短.
解答: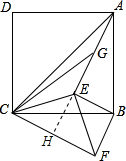 解:①根据旋转的性质知,△ABE≌△CBF,则BE=BF,所以△BEF为等腰直角三角形;故本选项正确;
解:①根据旋转的性质知,△ABE≌△CBF,则BE=BF,所以△BEF为等腰直角三角形;故本选项正确;
②∵∠AEB=90°,tan∠BAE=
,
∴AE=2BE.
又∵由①知,△ABE≌△CBF,
则BE=BF,AE=CF,∠CFB=∠AEB=90°,
∴BC=
BF=
BE.
∴S正方形ABCD=BC2=5BE2.
延长AE交CF于点H.
易证四边形EHFB为正方形,则BE=EH=HF=FB,
∴CH=CF-FH=AE-BE=BE.
∵点G是AE的中点,
∴8S△ECG=8×
S△ACE=8×
×
AE•CH=2×2BE×BE=4BE2<S正方形ABCD,
故本选项错误;
③∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠ECB=45°-∠ACE.
∵CH=HF,EH⊥CF,
∴∠CEH=∠FEH.
又∵由②知四边形EHFB为正方形,则∠HEF=45°,
∴∠CEH=45°,
∴∠CAG=∠CAE=∠CEH-∠ACE=45°-∠ACE,
∴∠ECB=∠CAG;
故本选项正确;
④在直角△GCH中,CH=BE,GH=2BE,则根据勾股定理知CG=
BE=BC,即CG=BC.
又∵四边形ABCD是正方形,
∴AD=BC,
∴CG=AD.
故本选项正确;
综上所述,正确的个数有3个;
故选C.
 解:①根据旋转的性质知,△ABE≌△CBF,则BE=BF,所以△BEF为等腰直角三角形;故本选项正确;
解:①根据旋转的性质知,△ABE≌△CBF,则BE=BF,所以△BEF为等腰直角三角形;故本选项正确;②∵∠AEB=90°,tan∠BAE=
| 1 |
| 2 |
∴AE=2BE.
又∵由①知,△ABE≌△CBF,
则BE=BF,AE=CF,∠CFB=∠AEB=90°,
∴BC=
| 5 |
| 5 |
∴S正方形ABCD=BC2=5BE2.
延长AE交CF于点H.
易证四边形EHFB为正方形,则BE=EH=HF=FB,
∴CH=CF-FH=AE-BE=BE.
∵点G是AE的中点,
∴8S△ECG=8×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故本选项错误;
③∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠ECB=45°-∠ACE.
∵CH=HF,EH⊥CF,
∴∠CEH=∠FEH.
又∵由②知四边形EHFB为正方形,则∠HEF=45°,
∴∠CEH=45°,
∴∠CAG=∠CAE=∠CEH-∠ACE=45°-∠ACE,
∴∠ECB=∠CAG;
故本选项正确;
④在直角△GCH中,CH=BE,GH=2BE,则根据勾股定理知CG=
| 5 |
又∵四边形ABCD是正方形,
∴AD=BC,
∴CG=AD.
故本选项正确;
综上所述,正确的个数有3个;
故选C.
点评:本题考查了全等三角形的判定与性质、正方形的判定与性质以及三角形面积的计算.注意,此题的辅助线的作法.

练习册系列答案
相关题目
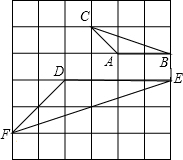 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.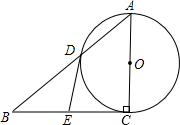 ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.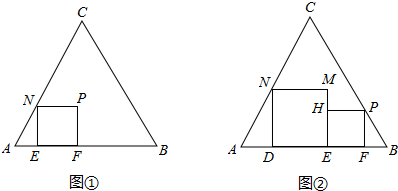
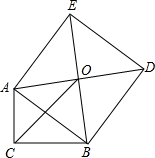 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6