题目内容
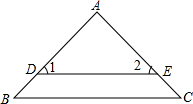如图，点D、E 分别在△ABC的边AB和AC上，且DE∥BC，∠1=∠2．问：△ABC是等腰三角形吗？请说明理由．
解：△ABC是等腰三角形，
理由是：∵DE∥BC，
∴∠B=∠1，∠C=∠2，
∵∠1=∠2，
∴∠B=∠C，
∴AB=AC，
∴△ABC是等腰三角形．
分析：根据平行线的性质推出∠B=∠1，∠C=∠2，推出∠B=∠C，根据等腰三角形的判定推出即可．
点评：本题考查了对等腰三角形的判定和平行线的性质的运用，关键是推出AB=AC，题目较好，难度不大．
理由是：∵DE∥BC，
∴∠B=∠1，∠C=∠2，
∵∠1=∠2，
∴∠B=∠C，
∴AB=AC，
∴△ABC是等腰三角形．
分析：根据平行线的性质推出∠B=∠1，∠C=∠2，推出∠B=∠C，根据等腰三角形的判定推出即可．
点评：本题考查了对等腰三角形的判定和平行线的性质的运用，关键是推出AB=AC，题目较好，难度不大．
练习册系列答案
金钥匙试卷系列答案
相关题目
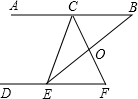如图，点C、E分别在直线AB、DF上，CF和BE相交于点O，CO=FO，EO=BO．
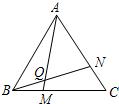25、如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60°．
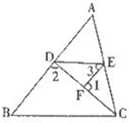30、如图，点D、E分别在△ABC的边AB、AC上，点F在DC上，且∠l+∠2=180°，∠3=∠B．求证：DE∥BC．
已知：如图，点D、E分别在AB、AC边上，△ABE≌△ACD，AC=15，BD=9，则线段AD的长是（ ）