题目内容
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(﹣6,7)、(﹣3,0)、(0,3).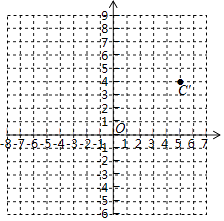
(1)画出△ABC,并求△ABC的面积;在△ABC中,点C经过平移后的对应点为C′(5,4),将△ABC作同样的平移得到△A′B′C′,画出平移后的△A′B′C′,并写出点A′,B′的坐标;
(2)P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),则m= , n= .
【答案】
(1)
解:如图,△ABC即为所求;△A′B′C′即为所求,A′(﹣1,8),B′(2,1)
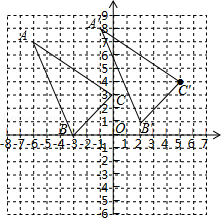
(2)﹣9;1
【解析】解:A′(﹣1,8),B′(2,1);(3)∵P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),
∴n=﹣3+4=1,m+6=﹣3,
∴n=1,m=﹣9.
故答案为:﹣9,1.
(1)根据各点在坐标系中的位置描出各点,并顺次连接即可;根据图形平移的性质画出平移后的△A′B′C′,并写出点A′,B′的坐标即可;(2)根据点平移的性质即可得出m、n的值.

练习册系列答案
相关题目