题目内容
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,它与
,它与![]() 轴、
轴、![]() 轴的交点分别为A、B两点.
轴的交点分别为A、B两点.
(1)求点A、B的坐标;
(2)设F是![]() 轴上一动点,⊙P经过点B且与
轴上一动点,⊙P经过点B且与![]() 轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与
轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与![]() 之间的函数关系;
之间的函数关系;
(3)是否存在这样的⊙P,既与![]() 轴相切,又与直线
轴相切,又与直线![]() 相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.
相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.

【答案】(1)A(﹣4,0),B(0,3); (2)y=![]() x2+
x2+![]() ; (3)存在.点
; (3)存在.点![]() 的坐标为(1,
的坐标为(1, ![]() )或(﹣9,15).
)或(﹣9,15).
【解析】试题分析:(1)根据坐标轴上点的坐标特征易得以A点坐标为(﹣4,0), B点坐标为(0,3),
(2)过点P作PD⊥y轴于D,则PD=![]() ,BD=
,BD=![]() ,根据切线的性质得PF=y,则PB=y,
,根据切线的性质得PF=y,则PB=y,
在Rt△BDP中,根据勾股定理得到y2=x2+(3﹣y)2 ,然后整理可得到:y=![]() x2+
x2+![]() ,
,
(3)因为⊙P与![]() 轴相切于点F,且与直线
轴相切于点F,且与直线![]() 相切于点B,根据切线长定理得到:AB=AF,而AB=5,所以AF=
相切于点B,根据切线长定理得到:AB=AF,而AB=5,所以AF=![]() 再把
再把![]() 分别代入y=
分别代入y=![]() x2+
x2+![]() 计算出对应的函数值,即可确定P点坐标.
计算出对应的函数值,即可确定P点坐标.
试题解析:(1)A点坐标为(﹣4,0),B点坐标为(0,3),
(2)过点P作PD⊥y轴于D,如图1,

则PD=|x|,BD=|3﹣y|,
∵⊙P经过点B且与x轴相切于点F,
∴PB=PF=y,
在Rt△BDP中,
∴PB2=PD2+BD2,
∴y2=x2+(3﹣y)2,
∴y=![]() x2+
x2+![]() ,
,
(3)存在.
如图2,∵⊙P与x轴相切于点F,且与直线l相切于点B,
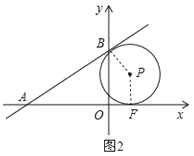
∴AB=AF,
∵AB2=OA2+OB2=52,
∴AF=5,
∵AF=|x+4|,
∴|x+4|=5,
∴x=1或x=﹣9,
当x=1时,y=![]() ,
,
当x=﹣9时,y=![]() =15,
=15,
∴点![]() 的坐标为(1,
的坐标为(1, ![]() )或(﹣9,15).
)或(﹣9,15).

练习册系列答案
相关题目