题目内容
若m=
是a+2的算术平方根,n=
是4+a2的立方根,求m+n的平方根.
| a+b | a+2 |
| 2a-1 | 4+a2 |
分析:根据算术平方根与立方根的定义,利用根指数列出等式求出a、b的值,然后代入进行计算求出m+n的值,再根据平方根的定义即可求解.
解答:解:根据题意得,a+b=2,2a-1=3,
解得a=2,b=0,
∴m=
=2,
n=
=2,
∴m+n=2+2=4,
∵(±2)2=4,
∴m+n的平方根是:±2.
故答案为:±2.
解得a=2,b=0,
∴m=
| 2+2 |
n=
| 3 | 4+22 |
∴m+n=2+2=4,
∵(±2)2=4,
∴m+n的平方根是:±2.
故答案为:±2.
点评:本题考查了算术平方根,立方根与平方根的定义,根据根指数列式求出a、b的值是解题的关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
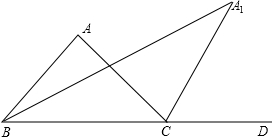
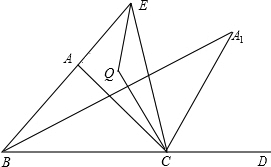
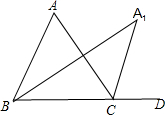 如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.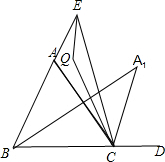
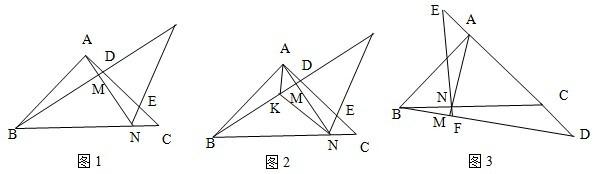
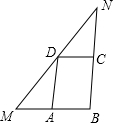 已知四边形ABCD为平行四边形,经过点D作直线MN,分别交BA、BC的延长线于点M、N,且∠NDC=∠MDA,若四边形ABCD的周长是4,则MB的长是
已知四边形ABCD为平行四边形,经过点D作直线MN,分别交BA、BC的延长线于点M、N,且∠NDC=∠MDA,若四边形ABCD的周长是4,则MB的长是