Question

【题目】如图，已知抛物线与直线AB相交于A（﹣3，0），B（0，3）两点．

（1）求这条抛物线的解析式；

（2）设C是抛物线对称轴上的一动点，求使∠CBA=90°的点C的坐标；

（3）探究在抛物线上是否存在点P，使得△APB的面积等于3？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）C（﹣1，4）；（3）（﹣1，4）或（﹣2，3）或（，）或（，）．

【解析】

试题分析：（1）把点A，B两点的坐标分别代入抛物线解析式，求出b和c的值即可；

（2）过点B作CB⊥AB，交抛物线的对称轴于点C，过点C作CE⊥y轴，垂足为点E，求出点C的横坐标，再求出OE的长，即可得到点C的纵坐标；

（3）假设在在抛物线上存在点P，使得△APB的面积等于3，连接PA，PB，过P作PD⊥AB于点D，作PF∥y轴交AB于点F，在Rt△OAB中，易求AB=，设点P的坐标为（m，），设点F的坐标为（m，m+3），再分两种情况讨论：①当点P在直线AB上方时，②当点P在直线AB下方时，分别求出符合条件点P的坐标即可．

试题解析：（1）把点A（﹣3，0），B（0，3）代入得：，解得：，∴抛物线的解析式是；

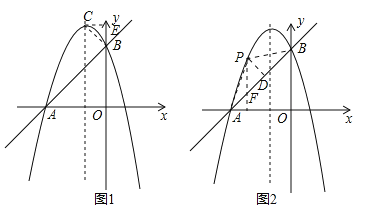
（2）如图1：过点B作CB⊥AB，交抛物线的对称轴于点C，过点C作CE⊥y轴，垂足为点E，∵，∴抛物线对称轴为直线x=﹣1，∴CE=1，∵AO=BO=1，∴∠ABO=45°，∴∠CBE=45°，∴BE=CE=1，∴OE=OB+BE=4，∴点C的坐标为（﹣1，4）；

（3）假设在在抛物线上存在点P，使得△APB的面积等于3，如图2：连接PA，PB，过P作PD⊥AB于点D，作PF∥y轴交AB于点F，在Rt△OAB中，易求AB==，∵S△APB=3，∴PD=，∵∠PFD=∠ABO=45°，∴PF=，设点P的坐标为（m，），∵A（﹣3，0），B（0，3），∴直线AB的解析式为，∴可设点F的坐标为（m，m+3），

①当点P在直线AB上方时，可得：，解得：m=﹣1或﹣2，∴符合条件的点P坐标为（﹣1，4）或（﹣2，3），

②当点P在直线AB下方时，可得：，解得：m=或，∴符合条件的点P坐标为（，）或（，）；

综上可知符合条件的点P有4个，坐标分别为：（﹣1，4）或（﹣2，3）或（，）或（，）．