题目内容
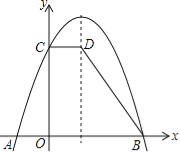
【题目】如图,已知抛物线与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C(0,3).
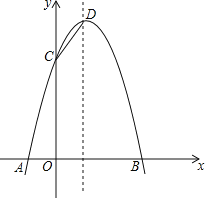
(1)该抛物线的对称轴是直线___________,
(2)求抛物线的解析式;
(3)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由:
【答案】(1)![]()
(2)![]() ;
;
(3)存在,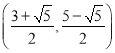 或(2.3)
或(2.3)
【解析】
(1)求出抛物线的解析式后,利用因式分解化成完全平方的形式,即可求出
(2)根据待定系数法,可得函数解析式;
(3)根据等腰三角形的判定,可得三角形三边的关系,分类讨论:PD=CD,根据勾股定理,可得x2+(3-y)2=(x-1)2+(4-y)2,根据图象上的点满足函数解析式,可得关于x的方程,根据解方程,可得答案;PD=CD时,根据对称性,可得答案.
(1)∵抛物线经过A(1,0)、B(3,0) 、C(0,3),
∴设抛物线解析式为![]() ,
,
根据题意,得
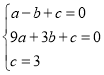 ,
,
解得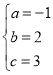 ,
,
∴抛物线的解析式为![]() ;
;
∴可以化为:![]()
∴该抛物线的对称轴是直线![]()
(2)由(1)可知,抛物线解析式为:![]()
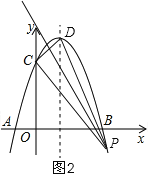
(3)存在, 由(1)可知,对称轴为![]() 所以D点坐标为(1,4),
所以D点坐标为(1,4),
当![]() 是等腰三角形时,分两种情况:
是等腰三角形时,分两种情况:
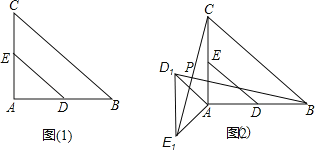
①当以CD为底边时,如图2,PD=PC,
设P(x,y),根据勾股定理,
则有:![]() ,
,
解得:![]() ,
,
∵P在抛物线上,
∴![]() ,
,
∴![]()
∴![]()
∴![]() ,
,
即:![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() ,
,
∴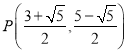 ,
,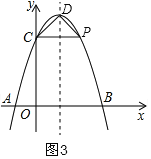
②当DC为腰时,如图3,则P、C关于直线x=1对称,
∴P(2,3),
综上所述,点P的坐标为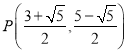 或(2,3).
或(2,3).

【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
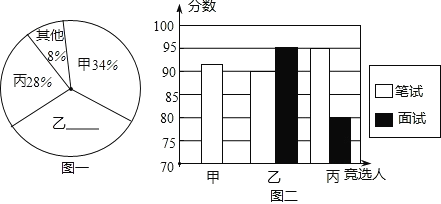
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?