题目内容
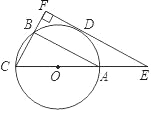
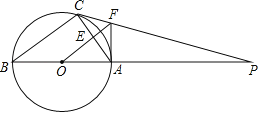
【题目】如图，
内接于
，AB是直径，的切线PC交BA的延长线于点P，
交AC于点E，交PC于点F，连接AF；
判断AF与的位置关系并说明理由．
若的半径为8，
，求AC的长．
【答案】（1）
为圆O的切线，理由见解析；（2）
．
【解析】
（1）AF为为圆O的切线，理由为：连接OC，由PC为圆O的切线，利用切线的性质得到CP垂直于OC，由OF与BC平行，利用两直线平行内错角相等，同位角相等，分别得到两对角相等，根据OB=OC，利用等边对等角得到一对角相等，等量代换得到一对角相等，再由OC=OA，OF为公共边，利用SAS得出三角形AOF与三角形COF全等，由全等三角形的对应角相等及垂直定义得到AF垂直于OA，即可得证；
（2）根据平行线的性质可知：OE垂直于AC，利用面积法求出AE的长，即可确定出AC的长．
为圆O的切线，理由是：
连接OC，
为圆O切线，
，
，
，
，
，
，
，
，
在
和
中，
，
≌
，
，
，OA为
的半径，
则AF为的切线；
是的直径，
，
，
，
，
，
在
中，
，
，
根据勾股定理得：
，
，
，
则
．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
