题目内容
27、自2007年1月1日起,某市全面推行农村合作医疗,农民每年每人只要拿出10元就可以享受到合作医疗.住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
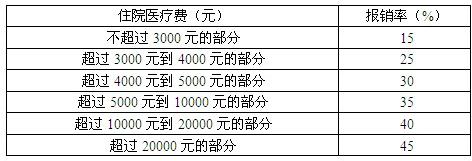
某人住院后得到保险公司报销的金额是805元,求此人住院的医疗费是多少?

某人住院后得到保险公司报销的金额是805元,求此人住院的医疗费是多少?
分析:先判断此人住院的医疗费在哪个范围之内,分别求出住院的医疗费是3000元时、住院的医疗费是4000元时、住院的医疗费是4000元时医疗报销金额分别是:450元、700元、1000元,由1000元>805元>700元,所以此人住院的医疗费超过4000元且小于5000元,以此人住院后得到保险公司报销的金额是805元为等量关系,列出方程求解.
解答:解:①住院的医疗费是3000元时,
得到保险公司报销的金额是:3000×15%=450(元),
②住院的医疗费是4000元时,
得到保险公司的报销金额是:3000×15%+1000×25%=700(元),
所以此人住院的医疗费超过4000元.
设住院的医疗费x(4000<x<5000)元,
可列方程:3000×15%+1000×25%+(x-4000)×30%=805,
解得:x=4350.
答:此人住院的医疗费是4350元.
得到保险公司报销的金额是:3000×15%=450(元),
②住院的医疗费是4000元时,
得到保险公司的报销金额是:3000×15%+1000×25%=700(元),
所以此人住院的医疗费超过4000元.
设住院的医疗费x(4000<x<5000)元,
可列方程:3000×15%+1000×25%+(x-4000)×30%=805,
解得:x=4350.
答:此人住院的医疗费是4350元.
点评:本题的关键在于理解题目的意思,先讨论此人的住院费用在那个范围之内,找出等量关系,列出方程求解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
为缓解油价上涨给出租车行业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数).
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元).如图,折线ABCD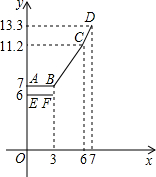 表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
①填空:a= ,b= ,c= ;
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象;
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元).如图,折线ABCD
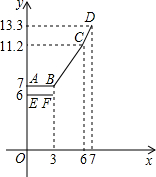 表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 | |
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象;
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
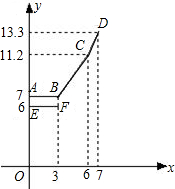 为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车待业带来的成本压力,某巿自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a 元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 |
①填空:a=
②写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
③函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在请说明理由.