题目内容
【题目】如图,在直角坐标系中,点A,B分别在射线Ox,Oy上移动,BE是∠ABy的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否为定值?请给出证明。
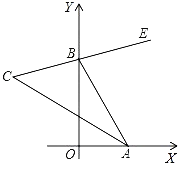
【答案】∠ACB的大小不发生变化,且始终保持45
【解析】
根据角平分线的定义、三角形的内角和、外角性质求解.
在纵轴B点上方任取一点为F,由BE平分∠ABF、CA平分∠OAB知2∠EBA=∠ABF、∠OAB=2∠CAB,根据△AOB外角性质得∠ABF=∠AOB+∠OAB,即∠ABF=90°+∠OAB,再根据△ACB外角性质得∠EBA=∠C+∠CAB,即90°+∠OAB=2(∠C+∠CAB),从而知90°+∠OAB=2∠C+∠OAB,即可得∠C=45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目