题目内容
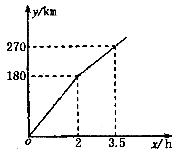
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:

(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.

(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求当x为多少时,两车之间的距离为300km.
(1)80,120 (2)D(4.5,360) (3)x="1.2" h或4.2 h
试题分析:(1)(480-440)÷0.5=80(km/h),
440 ÷2.2-80=120(km/h);
(2)快车到达乙地;
因为快车走完全程所需时间为480÷120=4(h),所以点D的横坐标为4.5,纵坐标为200×1.8=360,即点D(4.5,360);
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即(80+120) × (x-0.5)=440-300,解得x=1.2(h);
或(80+120) × (x-2.7)=300,解得x=4.2(h).
故x="1.2" h或4.2 h,两车之间的距离为300km.
点评:该题是常考题,主要考查学生通过观察横纵坐标表示的量对实际问题在直角坐标系表达意义的理解。

练习册系列答案
相关题目
 的图像交于A(2,2),B(-1,m),求反比例函数和一次函数的解析式.
的图像交于A(2,2),B(-1,m),求反比例函数和一次函数的解析式.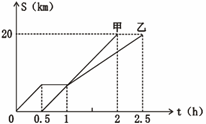
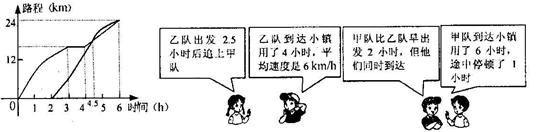
 的解集是
的解集是