题目内容
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0)，与y轴交于C（0，-3）
（1）求抛物线C1的表达式；
（2）分别写出抛物线C1关于B点，关于A点的对称抛物线C2， C3的函数表达式
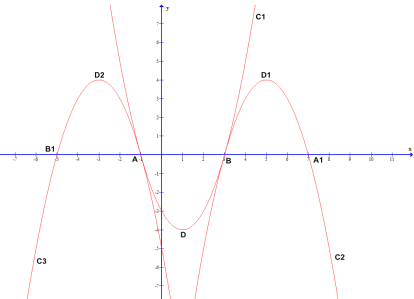
（3）设C1的顶点为D，C2与x轴的另一个交点为A1顶点为D1，C3与x轴的另一个交点为B1，顶点为D2，在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中，求面积最大的四边形的面积。
【答案】（1）抛物线C1的表达式为：y=x-2x-3；（2）抛物线C2表达式为：y2=-x2+10x-21；抛物线C3表达式为：y3= -x2-6x-5；（3）48.
【解析】
（1）将点B(3，0)，C（0，-3）代入y=x+bx+c求出b，c即可得到抛物线C1的表达式；
（2）求出A点坐标，可得AB=4，根据关于点成中心对称的图形的性质，可求出抛物线C2， C3的函数表达式；
（3）求出A、B、D、A1、B1、D1、D2这七个点的坐标，根据图形，计算几个面积较大的四边的面积，比较即可得到面积最大的四边形的面积.
解：（1）将点B(3，0)，C（0，-3）代入y=x+bx+c可得：
，
解得：
，
∴抛物线C1的表达式为：y=x-2x-3；
（2）令y=x-2x-3=0，解得：x1=3，x2=-1，
∴A（-1，0），
∴AB=4，
∴抛物线C2过点（3，0）和点（7，0）
设抛物线C2解析式为：y2=a(x-3)(x-7)，
∵抛物线C2与抛物线C1关于B点对称，
∴a=-1，即抛物线C2解析式为：y2=-(x-3)(x-7)=-x2+10x-21，
同理可得：抛物线C3解析式为：y3=-(x+5)(x+1)= -x2-6x-5；
（3）如图，由题意得：A（-1，0），B（3，0），A1（7，0），B1（-5，0），
∵抛物线C1：y=x-2x-3=(x-1)2-4，
∴D（1，-4），
同理：D1（5，4），D2（-3，4），
∴S梯形B1 D2 D1 A1=
，
S四边形B1D2DD1 = S四边形A1D1D2D =S平行四边形B1D2D1B+S△B1DB=
，
S四边形B1DA1D1 = S四边形A1DB1D2 =S△B1DA1+ S△B1A1D1=
，
（注：面积明显较小的四边形面积不予计算）
综上所述，面积最大的四边形的面积是48.
