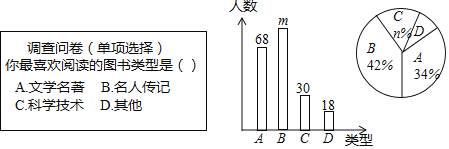
题目内容
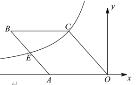
【题目】如图,在平面直角坐标系中,菱形 ABCO 的一边 OA 在 x 轴上,![]() ,反比例函数
,反比例函数![]() 过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
【答案】-2![]() .
.
【解析】
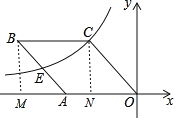
由菱形OABC的边长OA=3,可以表示出点A的坐标(-3,0),进而得出OA=AB=BC=CO=3,设出点C的坐标,表示出点B的坐标,再根据E是AB的中点,可以表示出点E的坐标,把点C、E的坐标代入反比例函数关系式,可求出a的值,即ON的长,再由勾股定理求出CN,确定b的值,进而求出k的值.
设C坐标为(a,b),
∵菱形ABCO的一边OA在x轴上,OA=3,
∴点B(a-3,b),
∵E是AB的中点,A(-3,0),
∴点E(![]() ,
,![]() ),
),
把点C、E的坐标代入反比例函数关系式得,
ab=k=![]() ×
×![]() ,
,
解得,a=-2,即ON=2,
∵OC=OA=3,
∴CN=![]() ,即,b=
,即,b=![]() ,
,
∴k=ab=-2×![]() =-2
=-2![]() ,
,
故答案为:-2![]() .
.

练习册系列答案
相关题目