题目内容
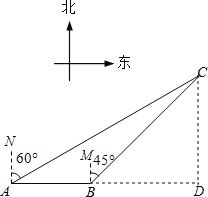
【题目】如图,大海中某岛C的周围25km范围内有暗礁.一艘海轮向正东方向航行,在A处望见C在北偏东60°处,前进20km后到达点B,测得C在北偏东45°处.如果该海轮继续向正东方向航行,有无触礁危险?请说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

【答案】该海轮继续向正东方向航行,无触礁危险.
【解析】试题分析:判断有无危险只要求出点C到AB的距离,与25海里比较大小就可以.首先过点C作CD⊥AB于点D,设BD=xkm,由三角函数的定义,即可求得CD=xkm,AD=![]() xkm,则可方程20+x=
xkm,则可方程20+x=![]() x,解此方程即可求得CD的长,比较即可求得答案.
x,解此方程即可求得CD的长,比较即可求得答案.
试题解析:
该海轮继续向正东方向航行,无触礁危险.
理由:过点C作CD⊥AB于点D,
∴∠BCD=∠CBM=45°,
设BD=xkm,则CD=![]() =x(km),
=x(km),
∵∠CAN=60°,
∴∠CAD=30°,
在Rt△CAD中,tan∠CAB=tan30°=![]() =
=![]() ,
,
∴AD=![]() CD=
CD=![]() x(km),
x(km),
∵AB=20km,AB+DB=AD,
∴20+x=![]() x,
x,
解得:x=10![]() +10(km),
+10(km),
∴CD=10![]() +10≈27.3(km)>25km,
+10≈27.3(km)>25km,
∴该海轮继续向正东方向航行,无触礁危险.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目






