Question

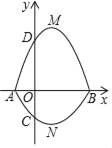
【题目】如图，抛物线C1：y＝mx2﹣2mx﹣3m(m＜0)与x轴交于A、B两点，与y轴交于点D，顶点为M，另一条抛物线C2与x轴也交于A、B两点，且与y轴的交点是C(0，)，顶点是N．

(1)求A，B两点的坐标．

(2)求抛物线C2的函数表达式．

(3)是否存在m，使得△OBD与△OBC相似？若存在，请求出m的值；若不存在请说明理由．

Answer 1

【答案】（1）A（﹣1，0），B（3，0）；（2）y＝．（3）m的值为﹣或﹣2．

【解析】

（1）解方程mx2﹣2mx﹣3m＝0可得到A，B两点的坐标；

（2）设交点式y＝a（x+1）（x﹣3），然后把C点坐标代入求出a得到抛物线C2的表达式；

（3）分两种情况考虑：当△OBD∽△OBC或△ODB∽△OBC时，求出OD长，得到m的值．

（1）当y＝0时，mx2﹣2mx﹣3m＝0，

∵x2﹣2x﹣3＝0，

∴x1＝﹣1，x2＝3，

∴A（﹣1，0），B（3，0）；

（2）设抛物线C2的表达式为y＝a（x+1）（x﹣3），

把C（0，﹣）代入，得a×1×（-3）=-，

解得a＝，

∴抛物线C2的函数表达式为y＝（x+1）(x-3)，

即y＝x2-x-．

（3）当△OBD∽△OBC时，= ，

∴OC＝OD，

∴D（0，）．

∴ -3m=，

∴m＝﹣，

当△ODB∽△OBC时，

=，

∴OD=9，

∴OD＝6，

∴D（0，6），

∴﹣3m＝6，

∴m＝﹣2，

综合以上可得m的值为﹣或﹣2．