��Ŀ����
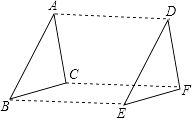
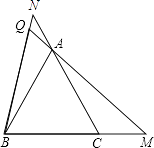
����Ŀ����һ�����dz���ͼƴ�ӣ���30��ǵ����dzߣ���ABC���ij�ֱ�DZ��뺬45��ǵ����dzߣ���ACD����б��ǡ���غϣ���֪AB��2 ![]() ��P��AC�ϵ�һ�����㣮
��P��AC�ϵ�һ�����㣮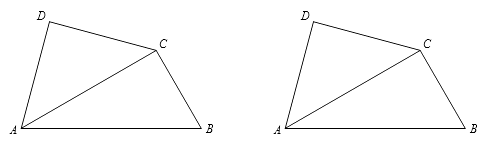
��1������P�˶�����ABC��ƽ������ʱ������DP��BP����CP��DP�ij���
��2������P���˶������г���PD��BCʱ�����ʱ��PDA�Ķ�����
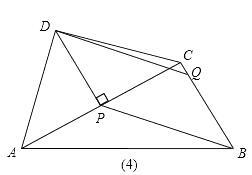
��3������P�˶���ʲôλ��ʱ����D��P��B��QΪ�����ƽ���ı��εĶ���Qǡ���ڱ�BC�ϣ������ʱƽ���ı��ε������
���𰸡�
��1��
�⣺��Rt��ABC�У�AB��2![]() ����BAC��30�㣬��BC��
����BAC��30�㣬��BC��![]() ��AC��3��
��AC��3��
��1����ͼ��1������DF��AC��
��Rt��ACD��AD��CD��
��DF��AF��CF��![]() ��
��
��BPƽ�֡�ABC��
���PBC��30�㣬
��CP��1��PF��![]() ��
��
��DP=![]() =
=![]() ��
��

��2��
�⣺��P��λ����ͼ��2����ʾʱ��
���ݣ�1���н��ۣ�DF��![]() ,��ADF��45�㣬��PD��BC=
,��ADF��45�㣬��PD��BC=![]() ��
��
��![]() ��
��![]() ��
��
���PDF��30�㣮
���PDA����ADF����PDF��15�㣮
��P��λ����ͼ��3����ʾʱ��ͬ��2���ɵá�PDF��30�㣮
���PDA����ADF����PDF��75�㣮
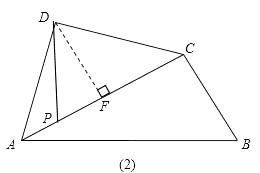

��3��
�⣺��BC��AC
��ֻ�е�DP��ACʱ����D��P��B��QΪ������ı���Ϊƽ���ı���.
��ͼ����DPBQ�У�BC��DP��
�ߡ�ACB��90�㣬
��DP��AC��
���ݣ�1���н��ۿ�֪��DP��CP��![]() ��
��
��SDPBQ��DP��CP��![]() ��
��
����������1����30�Ƚǵ�ֱ���������У����ߵı���1��![]() :2�����˿����CP������ֱ��������PDF�������PF��DE���������PD��
:2�����˿����CP������ֱ��������PDF�������PF��DE���������PD��
��2���������ۣ�P��DF��ߺ�P��DF�ұߣ�
��3��ֻ����DP//BC����DP=BC����DP��AC��CP��ƽ����DP��BC֮��ľ��룬��SDPBQ��DP��CP.