题目内容
【题目】已知抛物线
：
（m＞0）的顶点为M，交y轴于点G．
（1）如图，若点G坐标为(0，
)
①直接写出抛物线解析式；
②点Q在y轴上，将线段QM绕点Q逆时针旋转90°得线段QN，若点N恰好落在抛物线上，求点Q的坐标．
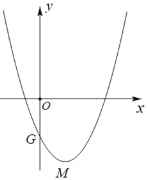
（2） 探究： 将抛物线沿唯一的定直线x=a对称得抛物线
，记抛物线交y轴于点P (0，－2m)，求a的值．
【答案】（1）①
；②Q1(0，
)，Q2(0，－
)；（2）1
【解析】
（1）①将点G的坐标代入到二次函数解析式中即可求出结论；
②设点Q（0，t），过点N作NA⊥y轴于点A，过点M作NB⊥y轴于点B，利用AAS证出△ANQ≌△BQM，求出二次函数图象的顶点坐标即可求出点N的坐标，然后将点N的坐标代入解析式中即可求出t的值，从而求出点Q的坐标；
（2）将二次函数的一般式转化为顶点式即可求出点M的坐标，然后求出抛物线
的顶点坐标，将点P的坐标代入得出关于a的一元二次方程，利用a有唯一值令△=0即可求出m的值，从而求出a的值．
解：（1）①将点G(0，
)代入解析式中，得
解得：m=1或-1（不符合条件，舍去）
将m=1代入解析式中，得
；
②设点Q（0，t），过点N作NA⊥y轴于点A，过点M作NB⊥y轴于点B，
∴∠NAQ=∠MBQ=90°，
又QM=QN，∠MQN=90°，
∴∠ANQ＋∠AQN=90°，∠BQM＋∠AQN=90°
∴∠ANQ=∠BQM
∴△ANQ≌△BQM，
∴AN=BQ，AQ=BM，
由点M
得M（1，
），即B（0，），
∴BM=AQ=1，BQ=AN=t+，
∴A（0，t+1)，即N（t+，t+1），
则有（t+）2－2（t+）－
=t+1，
解得t1=，t2=－，
∴Q1=（0，），Q2（0，－）
（2）解：
：
可化为
，
∴顶点M
，
又∵抛物线与抛物线关于直线x=a对称，由对称性知：
抛物线的顶点坐标为
，
∴抛物线的解析式为：
，
又∵抛物线交y轴于点 P (0，－2m)，
则有 
，
∴
而直线x=a唯一，
∴
，
解得，
所以有
，
解得，
