题目内容
【题目】如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则![]() 的值等于( )
的值等于( )
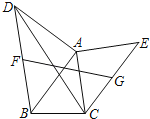
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
取BC的中点H,连接BE、FH、GH,求出∠BAE=∠DAC,然后利用“边角边”证明△ABE和△ADC全等,根据全等三角形对应边相等可得BE=CD,全等三角形对应角相等可得∠ABE=∠ADC,然后求出BE⊥CD,再根据三角形的中位线平行于第三边并且等于第三边的一半可得FH∥CD且FH=![]() CD,GH∥BE且GH=
CD,GH∥BE且GH=![]() BE,然后求出△HFG是等腰直角三角形,根据等腰直角三角形的性质可得
BE,然后求出△HFG是等腰直角三角形,根据等腰直角三角形的性质可得![]() ,然后求出
,然后求出![]() 的值即可.
的值即可.
解:如图,取BC的中点H,连接BE、FH、GH,
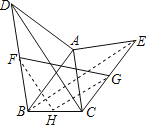
∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠BAE=∠DAC,
在△ABE和△ADC中,
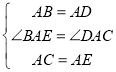 ,
,
∴△ABE≌△ADC(SAS),
∴BE=CD,∠ABE=∠ADC,
∴∠BDC+∠DBE=∠BDA+∠ABD=90°,
∴BE⊥CD,
又∵F、G分别是线段BD和CE的中点,
∴FH、GH分别是△BCD和△BCE的中位线,
∴FH∥CD且FH=![]() CD,GH∥BE且GH=
CD,GH∥BE且GH=![]() BE,
BE,
∴△HFG是等腰直角三角形,
∴![]() ,
,
∴![]() =
=![]() .
.
故选:B.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目