Question

【题目】如图，一次函数y=kx+b与反比例函数y=的图象在第一象限内交于A，B两点，点A的纵坐标为4，点B的坐标为（3，2），连接0A，OB．

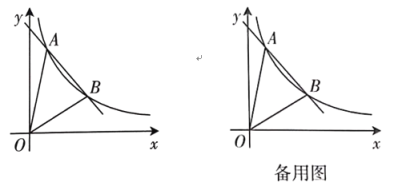
（1）求反比例函数的解析式；

（2）点M是线段AB上的一动点（不与点A，B重合），过点M作MEx轴于点E，作MNy轴为于点N，求四边形MEON 的最大面积；

（3）将直线y=kx+b向下平移n个单位长度，若直线与反比例函数在第一象限内的图象只有一个交点，求n的值．

Answer 1

【答案】（1）；（2）当时，四边形的面积最大，最大面积为；（3）．

【解析】

（1）把点代入反比例函数即可求解；

（2）先求出直线AB的解析式为，设点M的坐标为，得到，，则，根据二次函数的性质即可求出最大面积；

（3）设向下平移个单位长度后函数的解析式为，联立反比例函数得到一元二次方程，根据根的判别式即可求解．

（1）点在反比例函数的图象上，

∴.

∴反比例函数的解析式为.

（2）∵点的纵坐标为4，

∴，

设直线的解析式为y=kx+b（k≠0）

把、代入得

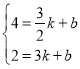，解得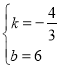

∴直线的解析式为.

∵点为线段上的一动点，

∴设点M的坐标为，.

∴，.

∴.

∴当时，四边形的面积最大，最大面积为.

（3）∵，

∴设向下平移个单位长度后函数的解析式为.

令，整理，得.

∵一次函数与反比例函数的图象在第一象限只有一个交点，

∴有唯一的实数根.

∴.

∴.

由题意得交点在第一象限内，

∴不符合题意，舍去.

∴．