题目内容
 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°,求∠BED的度数.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°,求∠BED的度数.
解:∵∠BDC是△ABD的外角,
∴∠ABD=∠BDC-∠A=60°-45°=15°.
∵BD是△ABC的角平分线,
∴∠DBC=15°
∵DE∥BC,
∴∠BDE=15°.
∴∠BED=180°-∠BDE-∠DBE=180°-15°-15°=150°.
分析:求∠BED的度数,应先求出∠ABC的度数,根据三角形的外角的性质可得,∠ABD=∠BDC-∠A=60°-45°=15°.再根据角平分线的定义可得,∠ABC=2∠ABD=2×15°=30°,根据两直线平行,同旁内角互补得∠BED的度数.
点评:本题考查三角形外角的性质及角平分线的定义和平行线的性质,解答的关键是沟通外角和内角的关系.
∴∠ABD=∠BDC-∠A=60°-45°=15°.
∵BD是△ABC的角平分线,
∴∠DBC=15°
∵DE∥BC,
∴∠BDE=15°.
∴∠BED=180°-∠BDE-∠DBE=180°-15°-15°=150°.
分析:求∠BED的度数,应先求出∠ABC的度数,根据三角形的外角的性质可得,∠ABD=∠BDC-∠A=60°-45°=15°.再根据角平分线的定义可得,∠ABC=2∠ABD=2×15°=30°,根据两直线平行,同旁内角互补得∠BED的度数.
点评:本题考查三角形外角的性质及角平分线的定义和平行线的性质,解答的关键是沟通外角和内角的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=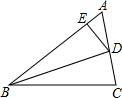 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是