题目内容
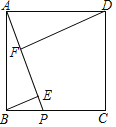
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC于E点,连接DE交OC于F点,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
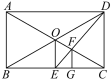
【答案】△ABC与△FGC是位似图形,位似中心是点C,△ABC与△FGC的相似比为3∶1.
【解析】
利用位似图形的性质得出位似中心,进而利用平行线分线段成比例定理求出即可;
△ABC与△FGC是位似图形,位似中心是点C.
因为在矩形ABCD中,AD∥BC,
所以∠FAD=∠FCE,∠FDA=∠FEC,
所以△AFD∽△CFE,
所以![]()
因为AD=BC,
所以![]()
因为∠ABC=90°,OE⊥BC,
所以OE∥AB.
因为OA=OC,
所以CE=![]() BC,
BC,
所以![]() =
=![]()
所以![]() =
=![]() .
.
即△ABC与△FGC的相似比为3∶1.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目