��Ŀ����
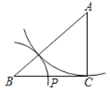
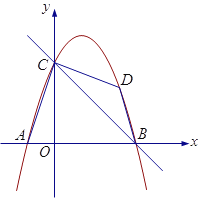
����Ŀ����ͼ��������y=ax2+bx+c��x���ཻ�ڵ�A����3��0����B��1��0������y���ཻ�ڣ�0����![]() ��������ΪP��
��������ΪP��
��1���������߽���ʽ��
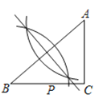
��2�����������Ƿ���ڵ�E��ʹ��ABP��������ڡ�ABE������������ڣ�������������ĵ�E�����ꣻ�������ڣ���˵�����ɣ�
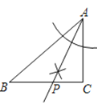
��3������ƽ�����Ƿ���ڵ�F��ʹ����A��B��P��FΪ������ı���Ϊƽ���ı��Σ�ֱ��д�����з��������ĵ�F�����꣬�����ƽ���ı��ε������
���𰸡���1��y=![]() x2+x��
x2+x��![]() ��2������������1��2
��2������������1��2![]() ��2����1+2
��2����1+2![]() ��2����3����F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ 8
��2����3����F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ 8
��������
��1���������߽���ʽΪy=ax2+bx+c��������3��0������1��0������0��![]() ���������a��b��c��ֵ���ɣ���2�����������߽���ʽ��֪����P�����꣬�����������εĵ���ͬ�ɵ�Ҫʹ���������������������ȣ�����P�������֪E�������꣬�������ʽ���x��ֵ���ɣ���3���ֱ�����ABΪ�ߡ�ABΪ�Խ�������������F�����겢���������ɣ�
���������a��b��c��ֵ���ɣ���2�����������߽���ʽ��֪����P�����꣬�����������εĵ���ͬ�ɵ�Ҫʹ���������������������ȣ�����P�������֪E�������꣬�������ʽ���x��ֵ���ɣ���3���ֱ�����ABΪ�ߡ�ABΪ�Խ�������������F�����겢���������ɣ�
��1���������߽���ʽΪy=ax2+bx+c��������3��0������1��0������0��![]() �����������߽���ʽ��
�����������߽���ʽ�� ��
��
��ã�a=![]() ��b=1��c=��
��b=1��c=��![]()
�������߽���ʽ��y=![]() x2+x��
x2+x��![]()
��2�����ڣ�
��y=![]() x2+x��
x2+x��![]() =
=![]() ��x+1��2��2
��x+1��2��2
��P����������1����2��
�ߡ�ABP��������ڡ�ABE�������
���E��AB�ľ������2��
��E��a��2����
��![]() a2+a��
a2+a��![]() =2
=2
���a1=��1��2![]() ��a2=��1+2
��a2=��1+2![]()
����������ĵ�E������Ϊ����1��2![]() ��2����1+2
��2����1+2![]() ��2��
��2��
��3���ߵ�A����3��0������B��1��0����
��AB=4
��ABΪ�ߣ�����A��B��P��FΪ������ı���Ϊƽ���ı���
��AB��PF��AB=PF=4
�ߵ�P���꣨��1����2��
���F������3����2��������5����2��
��ƽ���ı��ε����=4��2=8
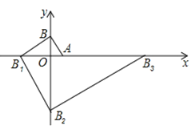
��ABΪ�Խ��ߣ���A��B��P��FΪ������ı���Ϊƽ���ı���
��AB��PF����ƽ��
���F��x��y���ҵ�A����3��0������B��1��0������P����1����2��
��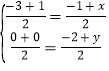 ��
��
��x=��1��y=2
���F����1��2��
��ƽ���ı��ε����=![]() ��4��4=8
��4��4=8
������������F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ8��

����Ŀ��Ϊ�ü������������н����һ���ƽ�ȫ���������С� �����������еĴ���������ѧУ����˫���������������룬��֯������������֪ʶ������ÿ������ͬ������ѧ���μӣ��ɼ��ֱ�Ϊ![]() �ĸ��ȼ�.������Ӧ�ȼ��ĵ÷����μ�Ϊ
�ĸ��ȼ�.������Ӧ�ȼ��ĵ÷����μ�Ϊ![]() �֡�
�֡�![]() �֡�
�֡�![]() �֡�
�֡�![]() �֣�ѧУ�����꼶��һ��Ͷ���ijɼ����������Ƴ�����ͳ��ͼ����
�֣�ѧУ�����꼶��һ��Ͷ���ijɼ����������Ƴ�����ͳ��ͼ����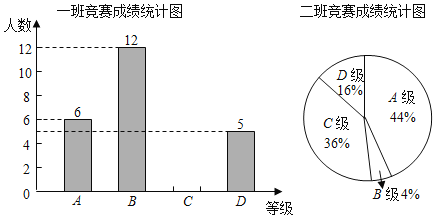
�༶ | ƽ�������֣� | ��λ�����֣� | �������֣� |
һ�� |
|
|
|
���� |
|
|
|
���������ṩ����Ϣ�����������:
(1)�벹ȫһ�ྺ���ɼ�ͳ��ͼ��
(2)��ֱ��д��![]() ��ֵ��
��ֵ��
(3)����Ϊ�ĸ���ɼ��Ϻã���д��֧����۵������.