题目内容
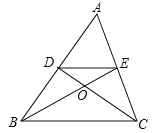
【题目】如图,△ABC≌△ADE,线段BC的延长线过点E,与线段AD交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B=48°,则∠DEF的度数_____.

【答案】36°
【解析】
由△ACB的内角和定理求得∠CAB=24°;然后由全等三角形的对应角相等得到∠EAD=∠CAB=24°.则结合已知条件易求∠EAB的度数;最后利用△AEB的内角和是180度和图形来求∠DEF的度数.
解:∵∠ACB=108°,∠B=48°,
∴∠CAB=180°﹣∠B﹣∠ACB=180°﹣48°﹣108°=24°.
又∵△ABC≌△ADE,
∴∠EAD=∠CAB=24°.
又∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=12°,
∴∠EAB=24°+12°+24°=60°,
∴∠AEB=180°﹣∠EAB﹣∠B=180°﹣60°﹣48°=72°,
∴∠DEF=∠AED﹣∠AEB=108°﹣72°=36°.
故答案为:36°

练习册系列答案
相关题目