题目内容
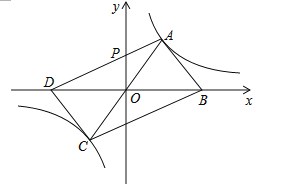
【题目】平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
【答案】(1)k=6,C(﹣2,﹣3);(2)![]() .
.
【解析】
试题分析:(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.
试题解析:(1)∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,∴3=
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,∴3=![]() ,点C与点A关于原点O对称,∴k=6,C(﹣2,﹣3),即k的值是6,C点的坐标是(﹣2,﹣3);
,点C与点A关于原点O对称,∴k=6,C(﹣2,﹣3),即k的值是6,C点的坐标是(﹣2,﹣3);
(2)∵△APO的面积为2,点A的坐标是(2,3),∴2=![]() ,得OP=2,设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,则
,得OP=2,设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,则![]() ,解得:
,解得:![]() ,即直线PC的解析式为
,即直线PC的解析式为![]() ,将y=0代入
,将y=0代入![]() ,得x═﹣4,∴OP=4,∵A(2,3),C(﹣2,﹣3),∴AC=
,得x═﹣4,∴OP=4,∵A(2,3),C(﹣2,﹣3),∴AC=![]() =
=![]() ,设点D到AC的距离为m,∵S△ACD=S△ODA+S△ODC,∴
,设点D到AC的距离为m,∵S△ACD=S△ODA+S△ODC,∴![]() ,解得,m=
,解得,m=![]() ,即点D到直线AC的距离是
,即点D到直线AC的距离是![]() .
.

【题目】某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如下表所示:
读书时间(小时) | 7 | 8 | 9 | 10 | 11 |
学生人数 | 6 | 10 | 9 | 8 | 7 |
则该班学生一周读书时间的中位数和众数分别是( )
A. 9,8 B. 9,9 C. 9.5,9 D. 9.5,8

